Rhombs with 3:1 Coloring
Why shoud we use sets of rhombs with exactly three sides same colored and one side colored with
another color? If three colors are given we get 12 pieces with the above property, which can cover a single
rhon with matching colors at the edges. Without this restriction we have too many rhombs and with only two colors
the number of pieces is too small. Therefore I started to examine also sest of such pieces with more given
colors. The sets are rather small due to the restriction and it wasn't that easy to get solutions for 7 colors or more.
3 Colors, 12 Pieces
Here are pictures of the 12 pieces and the covered rhon as physical object.

4 Colors, 24 Pieces
Two single rhons can be covered with this set.
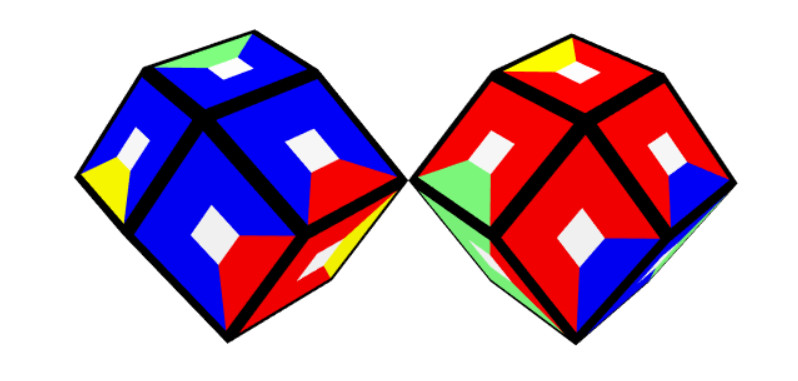
5 Colors, 40 Pieces
The square of size 2 is a special tetrarhon with 40 faces. Some other tetrarhons are also
connected at 4 faces and have a surface area of 4*12-4*2=40 faces.
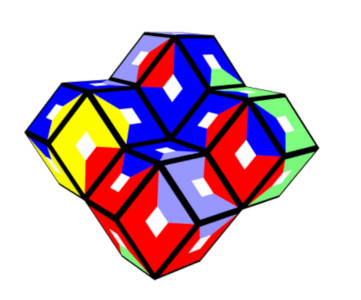
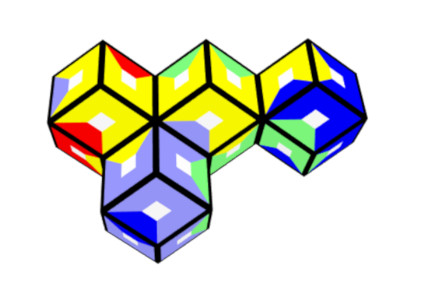
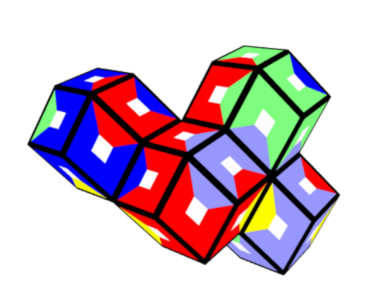
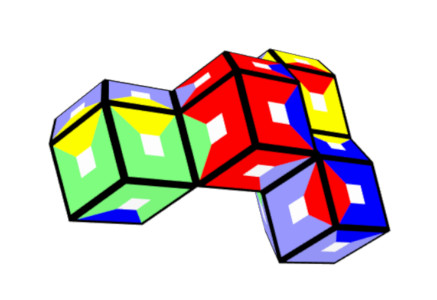
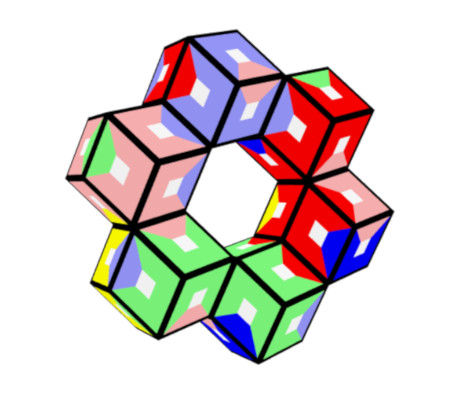
6 Colors, 60 Pieces
A hexagonal ring of size 2 and a hexagon of equal size both have a surface area of 40 faces,
because the center rhon of the hexagon hides 6 faces of the ring but contributes three additional faces each to the top and the bottom of the hexagon.
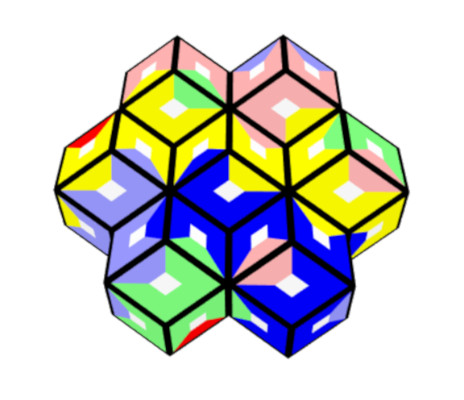
Among other figures a triangle with one rhon on top is possible.
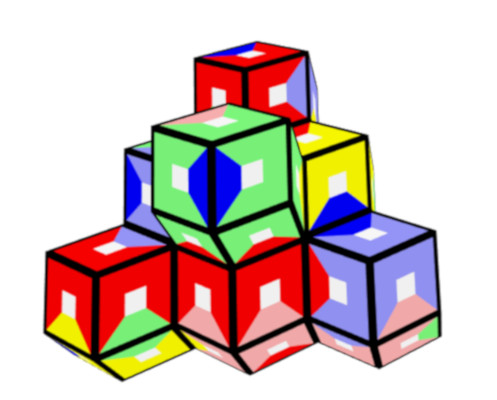
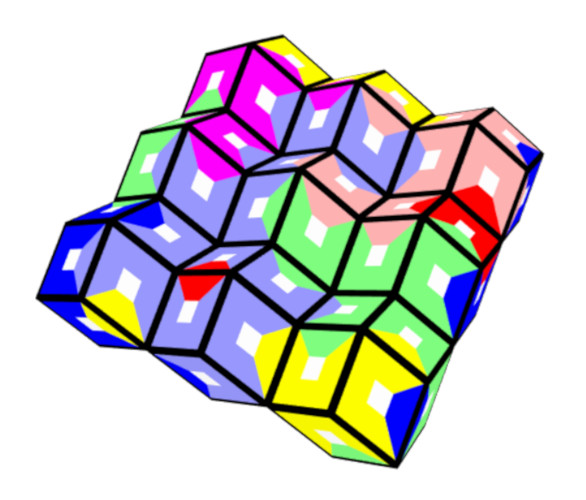
7 Colors, 84 Pieces
A highly symmetric figure is a square in the orthogonal grid.
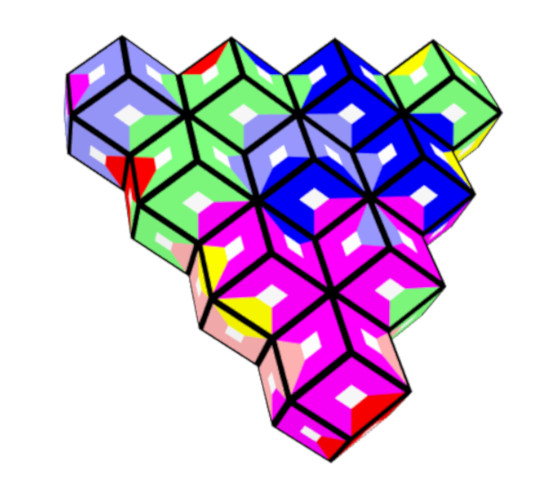
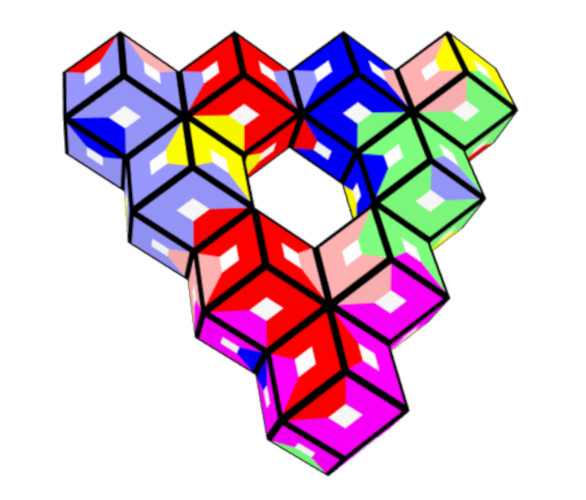
A triangular ring and a triangle of size 4 have the same number of faces.
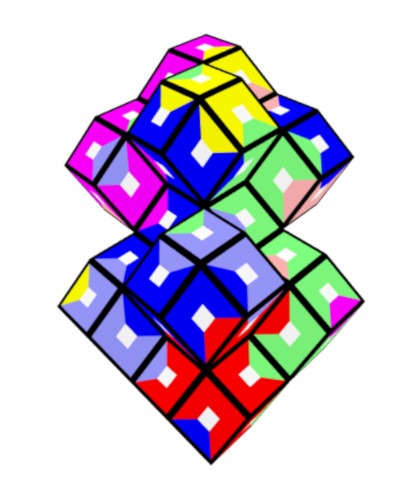
Two connected square pyramids and two joined octahedrons are examples for figures with more than one layer.
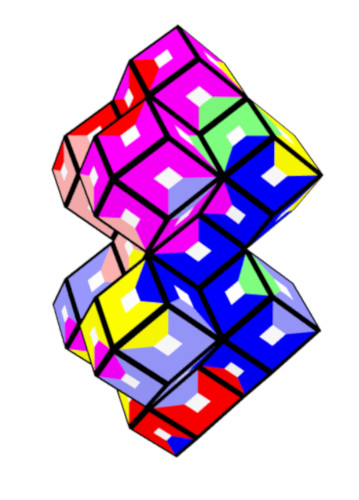
8 Colors, 112 Pieces
A chain of 11 rhons has 11*12-10*2=112 faces. From all these chains I covered the straight one with the
given pieces.

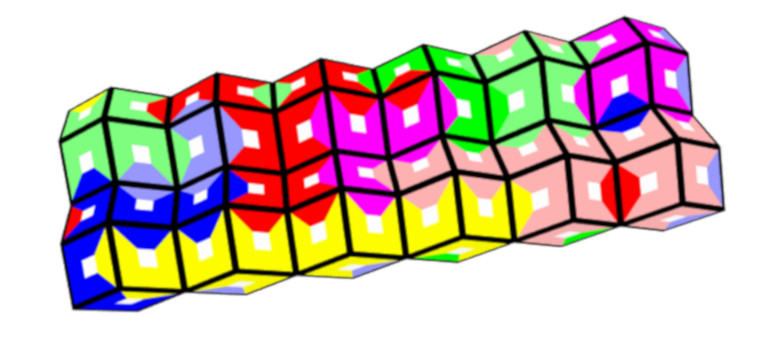
A 2x6 rectangle is also possible.
Back
Home
















