N Squares and One Sliced Square

2022/08/18

Two decades ago Andrew Clarke explored sets of sliced polyominoes, shown on his PolyPages. For some sliced rectangles like the one shown above a construction seemed to be hard or even impossible those days due to the length of the sliced side. Therefore I had a second look at these pieces and possible construction with them.

If you join n squares and one diagonal sliced square, called tan, you get as many different pieces as if you take (n+1)ominoes and remove one tan so that the pieces don't fall apart. These pieces are called n½ ominoes.

If only single cuts are allowed the set is slightly smaller and the pieces don't have interior angles of 315°. (S condition)

Otherwise you can take n-ominoes and extend these pieces by a tan. In this case the set is also slightly smaller because all pieces can't be made this way. (X condition)

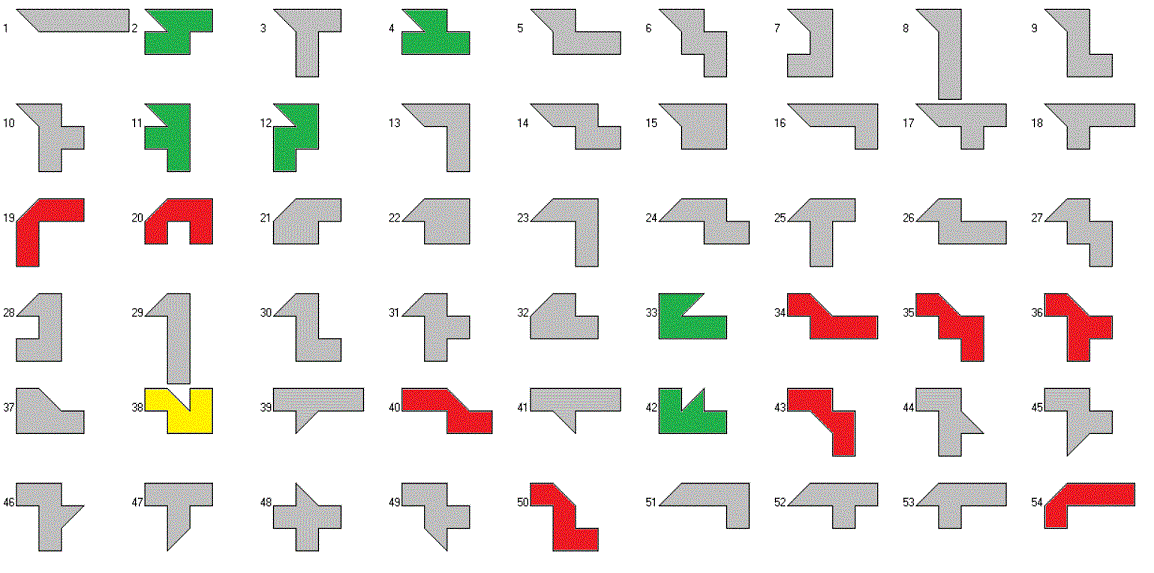
Therefore we can look for constructions with the whole set or subsets, where one or both conditions are met. For n=4 the whole set of two-sided pieces is shown. Pieces which violate the S, X or both conditions are marked green, red or yellow, respectively.

Click the numbers to see some construction with the different sets.

		Two-sided Pieces		One-sided Pieces
Number of Squares	Additional Property	Number of Pieces	Area	Number of Pieces	Area
3		14	49	27	94.5
	X	12	42	23	80.5
	S	13	45.5	25	87.5
	X & S	11	38.5	21	73.5
4		54	243	106	477
	X	44	198	88	396
	S	47	211.5	92	414
	X & S	38	171	76	342
5		210	1155	417	2293.5
	X	171	940.5	339	1864.5
	S	175	962.5	347	1908.5
	X & S	143	786.5	283	1556.5

Home