

Take n squares and connect them at their sides, at their corners or by long bridges skipping over a gap of one square. Jared McComb asked how many different pieces are possible. Let's have a look at the following arrangement of three squares. You can choose two out of three possible bridges to connect the squares getting two two-sided pieces or three one-sided pieces. A third bridge shouldn't be taken to avoid loops or holes for higher numbers of squares.
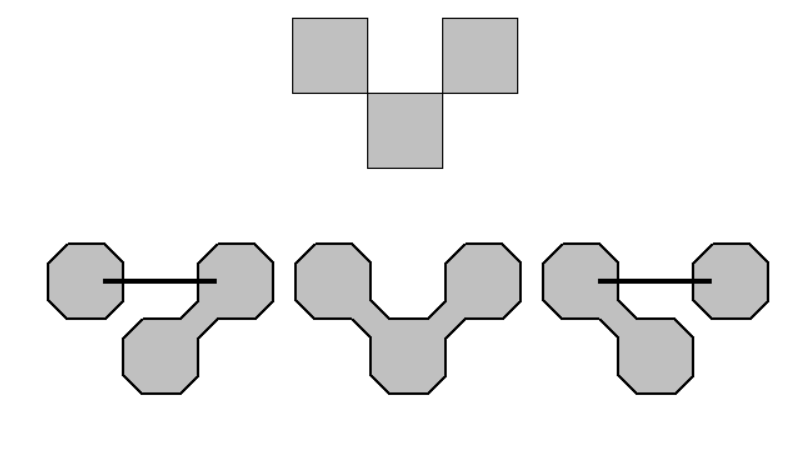
Therefore the bridges of the pieces must create a spanning tree with standard polyominoes as nodes and a fix number of squares. The table shows the number of pieces for a lot of sets. Click the numbers to see some constructions.
What's about physical pieces? The bridges between corners can be placed in the same layer as the polyominoes, if the corners of all squares are slightly cut off. The long bridges must be placed in additional layers getting problems with two-sided pieces, which demand space above and below the polyomino layer. Layer of transparent foil may do the job but I prefered one-sided pieces and printed them with a 3d-printer.

The table shows the number of pieces for different sets. Click the numbers to see some constructions and figures to solve.
| Number of Squares | Two-sided Pieces | Area | Constructions | One-sided Pieces | Area | Constructions |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | - | 1 | 1 | - |
| 2 | 3 | 6 | Hexominoes | 3 | 6 | Hexominoes |
| 3 | 11 | 33 | 11x3 rectangle, symmetric figures |
15 | 45 | Rectangles, pentomino models, rectangles with pentomino holes, symmetric figures |
| 4 | 91 | 364 | Rectangles and square rings with 90 pieces |
156 | 624 | Rectangles and rings with 155 pieces, Rectangles with 156 pieces and T-holes |
| 5 | 844 | 4220 | Snake 422x10 | 1614 | 8070 | Snake 807x10 |
| 1..4 | 106 | 404 | - | 175 | 676 | Four 13x13 squares |
Instead of squares you can also take rectangles with bridges skipping over the width or the height of them.
| Number of Rectangles | Two-sided Pieces | Area | Constructions | One-sided Pieces | Area | Constructions |
|---|---|---|---|---|---|---|
| 3 | 19 | 57 | Symmetric figures, 7x9 rectangles with hexomino holes |
30 | 90 | Rectangles, symmetric figures, rectangles with pentomino holes |
| 4 | 173 | 692 | Rectangle with 172 pieces | 310 | 1240 | Rectangle with 309 pieces |
