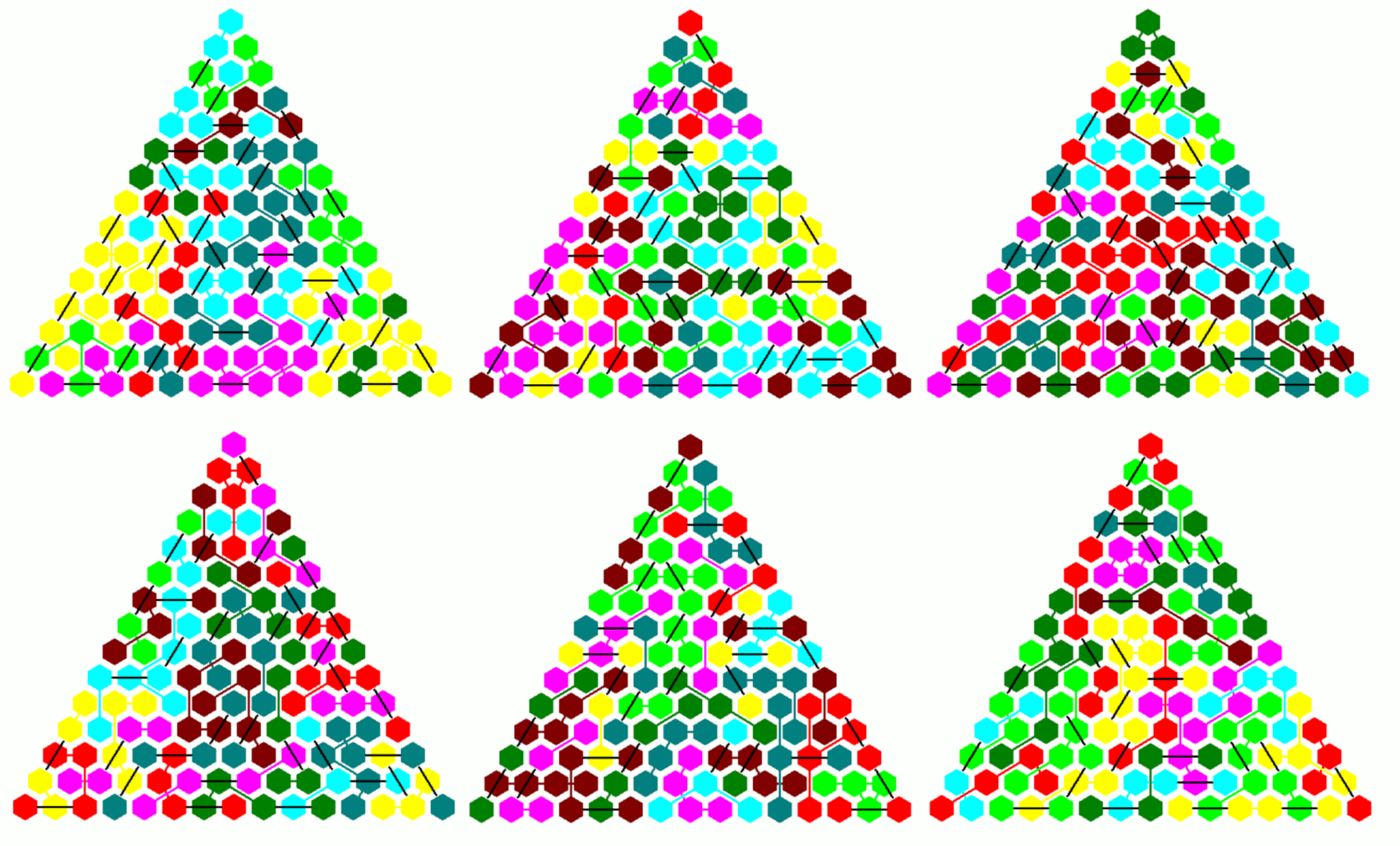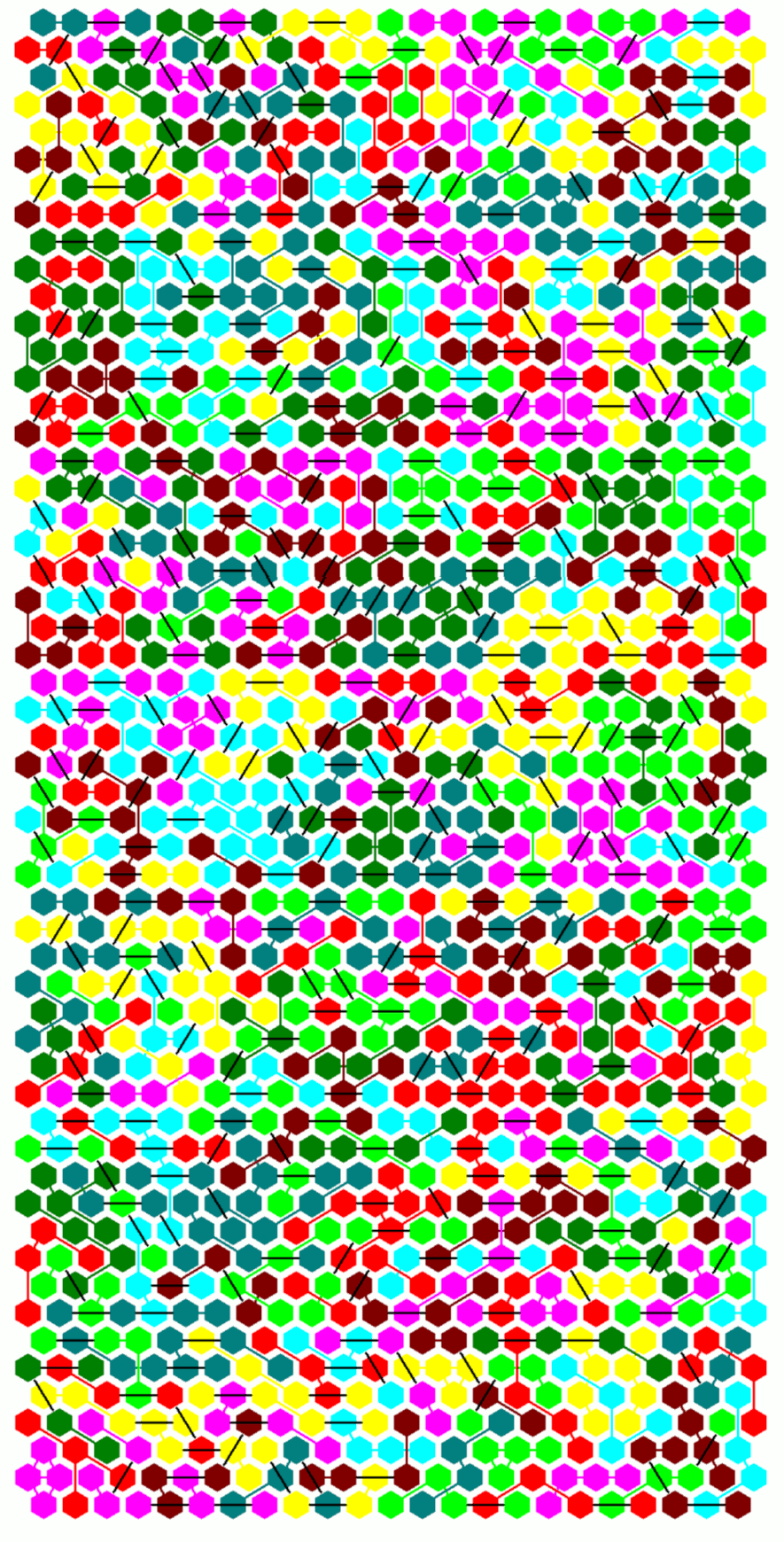Far Bridged Polyhexes

2023/03/13
Given a hexagonal grid with unit length 1 you can connect hexagons side by side getting ordinary polyhexes. Additional connections with distances of 3 between the centers of the hexagons leads to the
rounded or bridged polyhexes already discussed earlier. At last you may think of connections with distances of 2√ 3 between the centers of the hexagons, which skip over a whole hexagon. For the connections you need short bridges of length 1 and long bridges of length √ 3, respectively. The picture bewlow shows the three possible kinds of connections from the yellow hexagon. (sided by side with the green hexagons, short bridges to the red hexagons, long bridges to the blue hexagons)
How can we count the number of possible pieces? Since closed loops of short or long bridges prevent constructions without holes, the bridges should produce a spanning tree with ordinary polyhexes as components. Let's have a look at some pieces with four single hexagons and three long bridges,where the positions of the hexagons are all the same. We have 3 two-sided and 5 one-sided different pieces due to the selection of possible bridges.
How can we get physical pieces? For the one-sided pieces A-shaped bridges of different height and width can be added as shown in the title. But these pieces can't be turned upside down. Therefore I constructed hexagons of slightly smaller size to allow short bridges to pass bewtween the hexagons. Furthmore they get kind of grooves on the front and backside to create space for the long bridges. If you don't reduce the hexagons in size and add only additional grooves at the edges, you get problems combining some pieces as the following example shows. Take the piece with a 120° angle. The edges of the full size hexagons must go under the bridges of the I-piece but their own bridges must go above on the grooves of the I-piece.
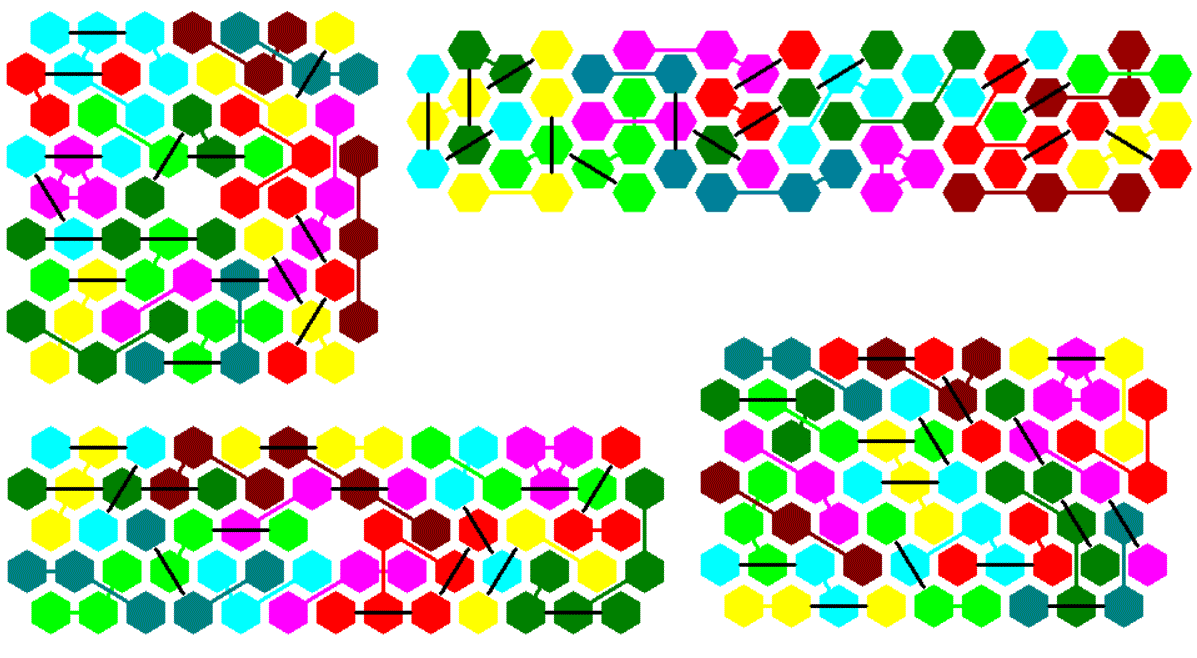
For sets of pieces with three and four hexagons I counted the number of pieces and made some symmetric constructions. Since the number of pieces grows very fast, we have already 2537 two-sided pieces with five hexagons. Click the sets in the table to see some examples for the smaller sets. The obj-files for the two-sided trihexes are here .
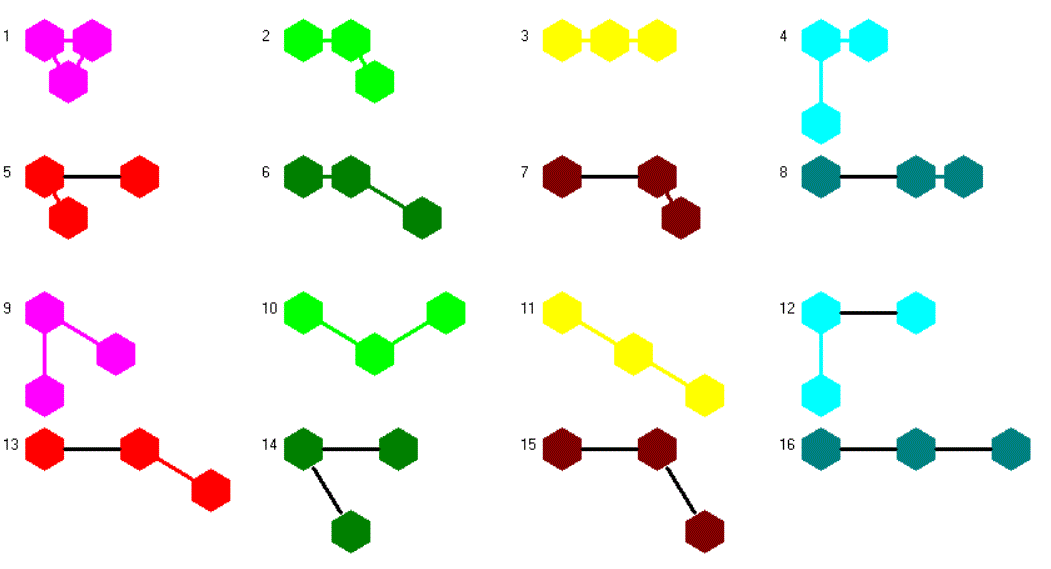
Two-sided Trihexes, 16 Pieces
Here are the 16 two-sided Trihexes with a total area of 48 hexagons. The long bridges are black colored, the short ones have the same color as the hexagons. Since the hexagons are smaller than the grid size, touching sides are connected by a very short line of same color.
The solid pieces are shown with bridges at the bottom. Turning them upside down the bridges are in the top layer. This allows constructions, where a single hexagon is skipped by two bridges, one below and one above it. This way you get more options to finish a construction. Because there are only 16 pieces it seems to be possible to solve some problems by hand.
For each kind of symmetry one construction with the printed pieces is shown and some other figures are added.
Symmetry under 60 ° Rotation
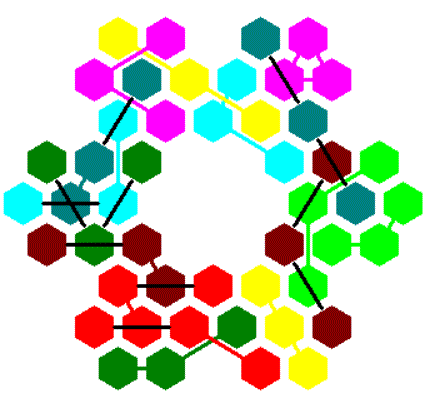
Since 48 is a multiple of 6 some figures with center holes and hexagonal symmetry are possible. If you don't allow bridges over empty places it's an addtional condition and the constructions might be more difficult but the solutions look a little bit nicer.
In the picture above one hexagon has two crossing bridges. Among the following constructions the second one has a bridge skipping over the empty center, but a solution without such a skipping bridge is also possible.
The next construction has crossing bridges. This makes a figure possible without bridged empty places.
Symmetry under 120 ° Rotation
To get figures with triangle symmetry you can start with a triangle of size 10 and an area of 55 hexagons. Then you can remove 7 hexagons from the center or one hexagon from the center and 3*2 hexagons from the border.
You can also modify a triangle of size 9 or you can combine three rhombs of size 4x4. Chains of rhombs may also be possible but in some cases you might need crossing bridges or bridges skipping empty places.
Two Axes of Symmetry
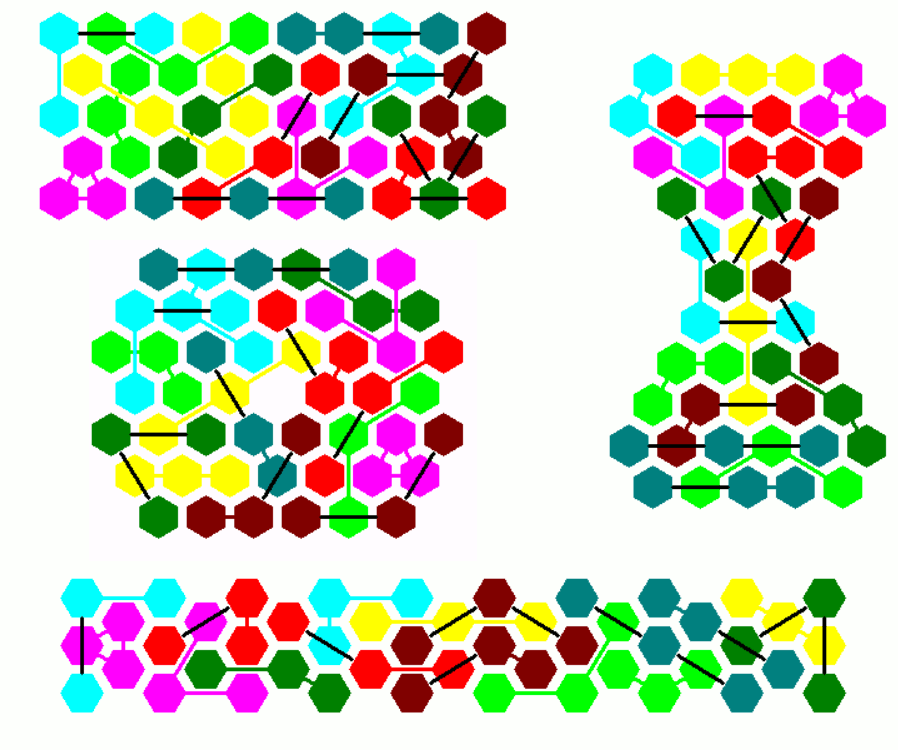
Since 48=49-1 we have a rhomb of size 7 with a center hole.
Kind of rectangles are made from y rows with x hexagons and y-1 rows of x-1 hexagons. The picture shows two rectangles of this type.
Symmetry under 180 ° Rotation
A parallelogram of size 11x5 with a hexagonal hole is shown with the real pieces. A parallelogram of size 10x5 with a 2x1 hole, which is a kind of similar hole figure, is also possible.
Among the constructions without holes are parallelograms of size 16x3, 12x4 and 8x6.
One Axis of Symmetry
There is only one trapezium to construct.
Here are a few examples for figures with one axis of symmetry. Other chains of trapezia even with two axes of symmetry seem to be possible.
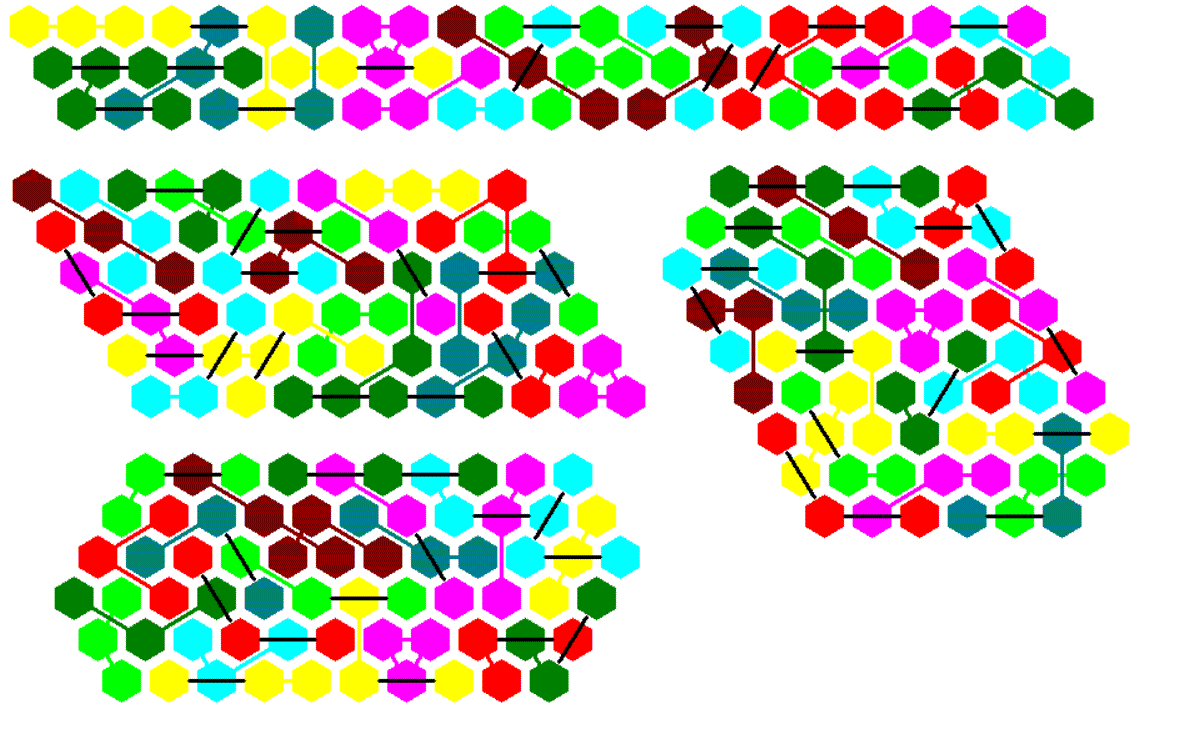
One-sided Trihexes, 22 Pieces
Here are the 22 one-sided far bridged Trihexes with a total area of 66 hexagons.They can be sorted by the following properties: number of bridges, type of bridges, angle between bridges. This way it's easy to spot a special piece and its mirror piece in a given figure or set.
The printed pieces are rather fragile, because the bridges are too thin and they don't stick perfectly to the hexagons.
Symmetry under 60 ° Rotation
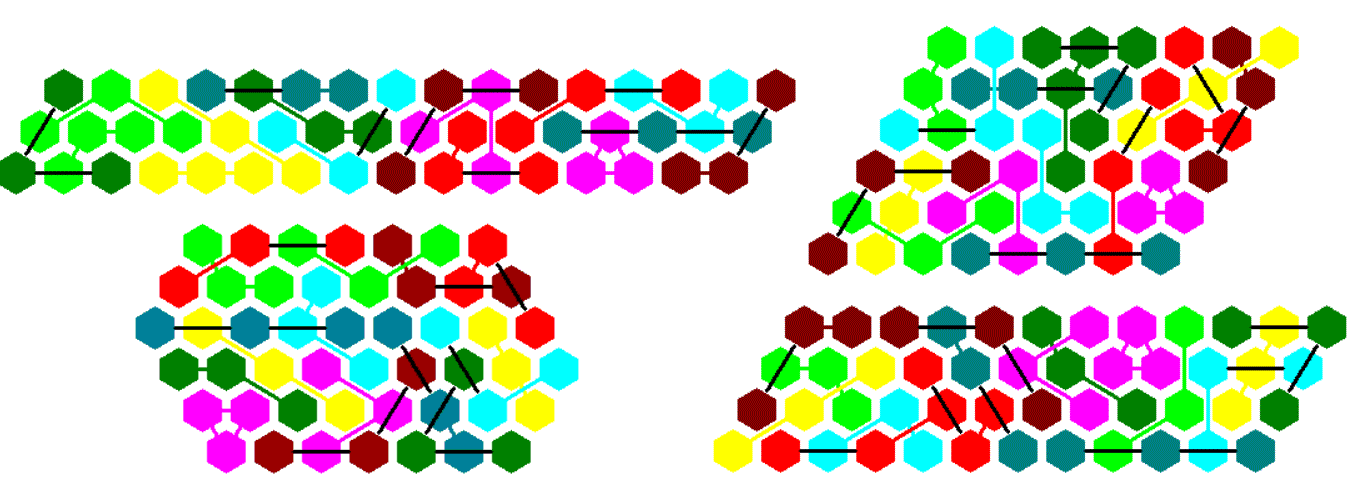
The construction is based on a regular hexagon with a hexagonal hole. This ring consists of 61-19=42 hexagons. Now we can distribute the remaining 66-42=24 hexagons at the corners, as shown, or at the sides.
You can also take a hexagon with a side length of 4 and remove a single hexagon or seven hexagons from the center. Remaining hexagons must be distributed symmetrically.
Symmetry under 120 ° Rotation
In the title a triangle made from all pieces is already shown.
In the picture below there are three smaller triangles of size 6 which are connected at their corners by single hexagons to get a large triangle with a large hole. You can also construct three triangles of same size, which are not connected. If the triangle piece with no bridges is left, a tristar is possible.
The shown tristars can also be constructed using three congruent parts and the triangle pieces. Removing congruent parts from the corners of larger triangles yields some other symmmetric figures.
Two Axes of Symmetry
I looked for kind of jagged rectangles with N(a,b)=a*b+(a-1)(b+1) hexagons. If N(a,b)=66 we can made rectangles with no holes. If N(a,b)=67 a single hole in the center is needed.
Symmetry under 180 ° Rotation
Given a 17x4=68 parallelogram you can remove single hexagons at two opposite corners and you'll get a kind of hexagon, symmetric under 180 ° rotation.
Since 66=2*3*11 the only possible parallelograms are 22x3 and 11x6. Cutting triangles of size 2 from opposite corners of larger parallelograms leads to other symmetric constructions.
One Axis of Symmetry
Here are two triangles of size 6 and one triangle of size 8, which are connected. It's also possible to construct the three triangles unconnected to get other symmetric figures with other arrangements of the parts.
There are only two trapezia possible. Cutting congruent triangles from the bottom corners of larger trapezia or triangles allows to make kind of hexagons or one pentagon with one axis of symmetry.
Two-sided Tetrahexes, 180 Pieces
Far bridged tetrahexes consist of four hexagons, but the positions of these hexagons can be more distant in the hexagonal grid than the positions in the case of ordinary polyhexes. Therefore tileability of figures is much worse and the number of pieces higher. Here are the 180 two-sided pieces.
Symmetry under 60 ° Rotation
I noticed that the total area of 720 hexagons is just enough to fill a hexagon od size 16. You should split the whole hexagon into some stripes, because such stripes are easier to fill. First you must use as many bad pieces as possible, wheras the pieces with high tileability are saved for the last parts.
Six Congruent Triangles
We can also divide the hexagon into six congruent triangles but it's harder to get a solution. There are three sharp corners to fill, and starting at the bottom the rows are longer than the columns in the solution with stripes. But at last I got a solution.
One-sided Tetrahexes, 323 Pieces
Two Axes of Symmetry
We have 323 one-sided pieces with a total area of 1292. Hexagonal symmetry isn't possible, because (1292-1)/6 isn't an integer. I looked for kind of rounded rectangles of size a*b+(a-1)(b+1)=1292. We have the following solutions:
Click the numbers to see the constructions.
Rectangle 3x258+2x259
The figure is divided into six same sized parts and two smaller ones. At first parts 1 to 5 were solved, then the smaller parts and at last part 6. A first approach to solve the smaller parts at last didn't work.
Rectangle 24x27+23x28
The whole figure was divided into stripes of eight rows. I think you can see the separating lines.
Rectangle 28x23+27x24
Stripes of eight rows can be easily combined to fill a large part of the whole rectangle.
Rectangle 259x2+258x3
Such a construction isn't possible. The straight piece with three long bridges doesn't fit into the very small pattern.
Home