

Beside the Platonic solids the Catalan solids are convex solids with congruent faces and fixed dihedral angles. We can use polygons with colored sides to cover the solids so that same colored sides match at the edges of the solid. If the set of polygons is large enough, this is no problem. Therefore I looked for sets with special properties, so that the number of pieces in the set is equal to the number of faces of a given Catalan solid. In most cases it was easy for my computer program to get a solution, only in case of the pentagonal hexecontahedron a solution wasn't found immediately.
Because of the fixed dihedral angles you can print the congruent polygons with fixed bevels and then glue all of them to get the Catalan solid.
It's also possible to add kind of folds and gaps at these folds to connect the polygons by U-clips. The positions for the gaps are: center (0), right from center (1), left from center (-1), far right from center (2) and far left from center (-2). A gap x then matches a gap -x. At the virtual objects the center positions are always red marked, left and right positions are blue marked and the more distant positions are green marked. Since the sides of the polygons are of different length, equal positions divide the sides by fixed ratios.
Because there are dipyramids and antidipyramids with congruent faces and fixed dihedral angles I also had a look at some of these pyramids.
Click the pictures in the table to see examples of covered Catalan solids and the used sets. If you click these examples you can also see virtual models ot them.
This is a real solid where the marks are replaced by gaps, and the triangles are connected at these points.
This is a real solid where the marks are replaced by gaps, and the triangles are connected at these points.
This is a real solid where the marks are replaced by gaps, and the triangles are connected at these points.
Following a computer solution sets of six triangles each were arranged getting eight larger kind of triangles. These parts can be
combined to get the whole construction.
This is a real solid where the marks are replaced by gaps, and the triangles are connected at these points.
This is a real solid where the marks are replaced by gaps, and the kites are connected at these points.
After I had glued a rhombic triacontahedron I stuck iron foil on the faces. Then printed colored rhombs
were stuck on magnetic foil to put them onto the solid.
The rhombs can also be used to fill a parallelogram of size 5x6.
This is a real solid where the marks are replaced by gaps, and the kites are connected at these points.
This is a real solid where the marks are replaced by gaps, and the pentagons are connected at these points.
These are the parts of the real solid, where the marks are replaced by gaps, and the pentagons are connected at these points. OBJ-files to print the 60 pentagons are here.
Triakis Tetrahedron

Triakis Octahedron
Triakis Icosahedron

Tetrakis Hexahedron
Pentakis Dodecahedron

Hexakis Octahedron
Since the 48 congruent faces of the hexakis octahedronare are scalene triangles we have 24 pairs of mirror pieces. For each coloring of one triangle there is a reflected coloring of the mirror piece.


Hexakis Icosahedron
Since the 120 congruent faces of the hexakis icosahedron are scalene triangles we have 60 pairs of mirror pieces. For each coloring of one triangle there is a reflected coloring of the mirror piece.
Dipyramids
Rhombic Dodecahedron

Rhombic Triacontahedron


Deltoidal Icositetrahedron
one-sided kites,
4 possible colors,
all sides differently colored,
4*3*2*1=24 pieces
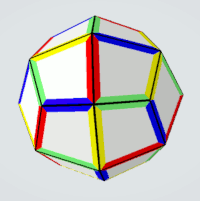
one-sided kites,
4 possible positions for marks,
all positions are different,
4*3*2*1=24 pieces
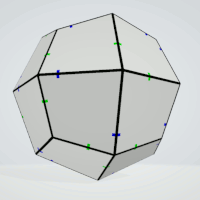

Deltoidal Hexecontahedron
one-sided kites,
5 possible colors,
two pairs of same colored sides,
3*(5*4)=60 pieces
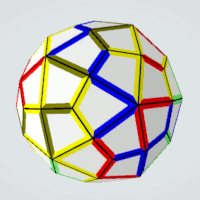
one-sided kites,
5 possible positions for marks,
two pairs of sides with equal positions,
3*(5*4)=60 pieces
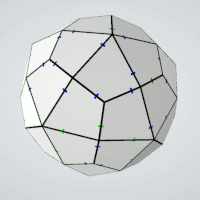
Antidipyramid
Pentagonal Icositetrahedron

Pentagonal Hexecontahedron
