Colored Polyiamonds
2016/10/05

A long time ago I made some constructions with edge-colored squares, triangles, hexagons and rhombs. Jared McComb
noticed that the rhombs are diamonds or polyiamonds of order 2 and suggested to explore the sets of edge-colored
triamonds. As usual touching edges must have the same color and the border of a construction should be uniformly
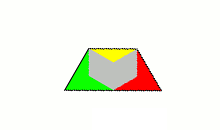
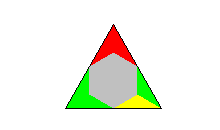
colored. Using only two colors for the triamonds we get 32 one-sided pieces and the hexagon shown above can be made.
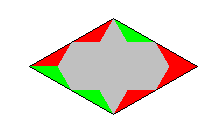
Tetriamonds can also be colored. If you take the triangular tetriamond and n colors, you get a similar problem as
if you take a single triangle and n^2 colors. If you have the two colors red and green,
you can make the following assignment rr-1, rg-2, gr-3, gg-4. But now the matching conditions are 1-1, 2-3, 3-2 and
4-4 contrary to the usual conditions for 4 colors. The numbers of pieces are equal, but the solutions are
different.
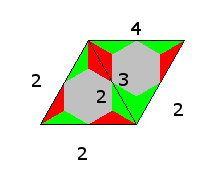
Furthermore I colored the straight tetriamond and the rhombic octiamond.
Click the shapes to see the sets and constructions.
Home