Polyhexes in a 3-Colored Hexagonal Grid

2023/05/05
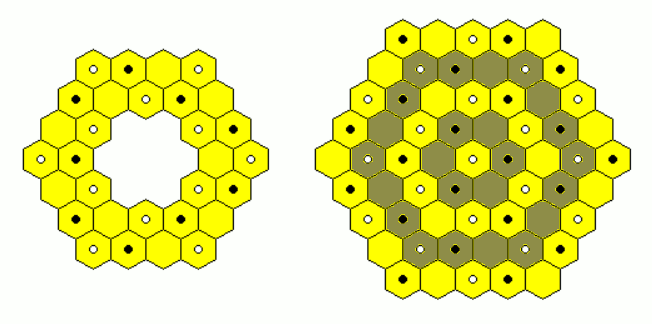
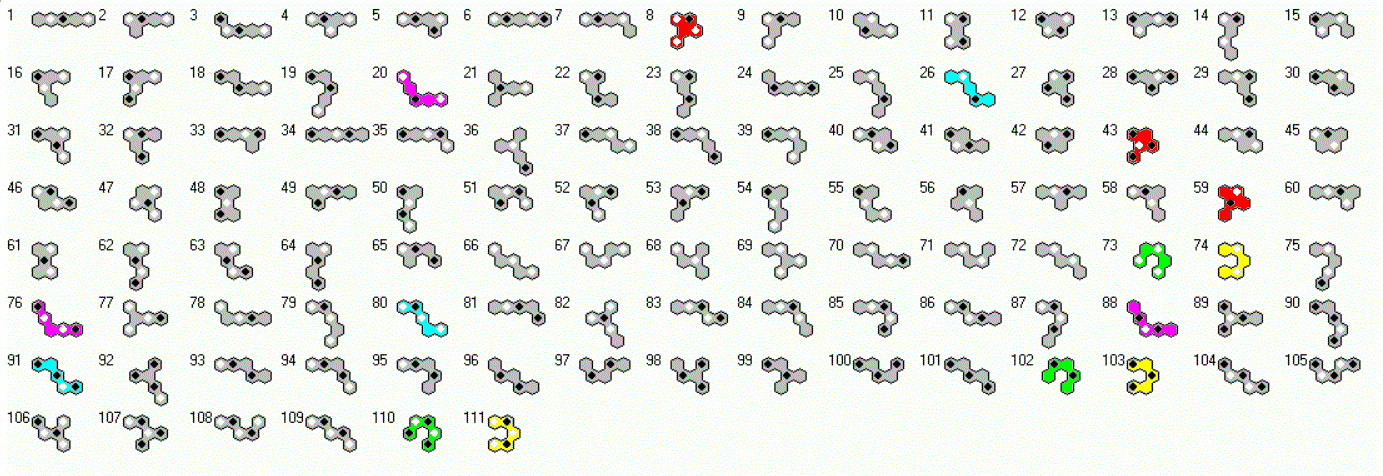
Polyhexes are made up from N regular hexagons joined at their sides. It's possible to cut out these pieces from a hexagonal grid. If the grid has a periodic coloring using three colors, same shaped pieces can get different colorings. Instead of three trihexes we get 10 different two-sided pieces. We have six arcs, three straight trihexes and one triangular shaped piece. For the last one a second piece is posssibe, if one-sided pieces are considered.
If you construct a figure with these pieces, the colors of the pieces should match the colors of the grid. So if all pieces are used, it's necessary that the numbers of same colored positions of the figure must be equal.
Instead of three colors for the grid you can also use three kinds of hexagons as shown above.
I created pieces up to six hexagons and looked for symmetric figures, which are possible to construct. The table shows the numbers of one-sided and two-sided pieces and for comparison the number of the ordinary polyhexes. Click the numbers to see some constructions.
|
Number of Two-sided Pieces |
|
Number of One-sided Pieces |
|
| Number of Hexagons |
without Color |
with Color |
Total Area |
without Color |
with Color |
Total Area |
| 2 |
1 |
3 |
6 |
1 |
3 |
6 |
| 3 |
3 |
10 |
30 |
3 |
11 |
33 |
| 2 or 3 |
4 |
13 |
36 |
4 |
14 |
39 |
| 4 |
7 |
30 |
120 |
10 |
48 |
192 |
| 5 |
22 |
111 |
555 |
33 |
186 |
930 |
| 6 |
82 |
435 |
2610 |
147 |
816 |
4896 |
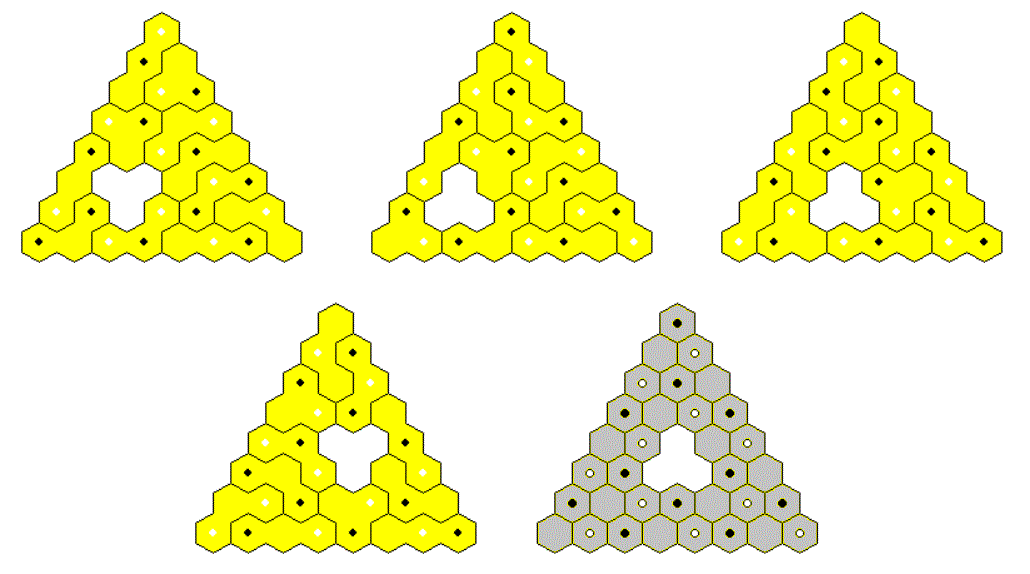
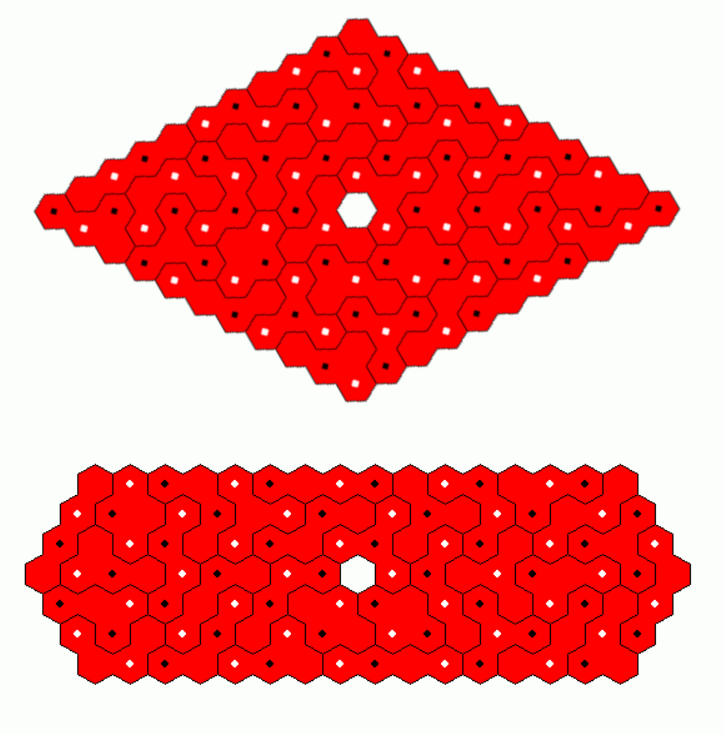
Two-sided Trihexes, 10 Pieces
These are the printed pieces with a total area of 30 hexagons; the obj-files for these pieces are here. The three colors are replaced by three kinds of hexagons: solid, only border and with diagonals. The set is rather small and suitable to construct a lot of figures by hand.
Since 30=3*10=5*6 we can make two parallelograms.
Solving a(a+1)/2-b(b+1)/2=30 for integer values a, b we can get three trapezia.
We can further look for figures symmetric under 120° rotation with or without three axes of symmetry.
A small hole of three hexagons at the center of rotational symmetry is also possible.
In the following similar hole figure the triangular hole must be placed at the center of the larger triangle.
Unfortunately the ring shown below cannot be constructed, because the numbers of hexagons with same color don't equal 10. Any other figure with hexagonal symmetry cannot be done either, because the number of white hexagons in every ring are multiples of 3, so that we can't place the 10 white hexagons of the whole set.
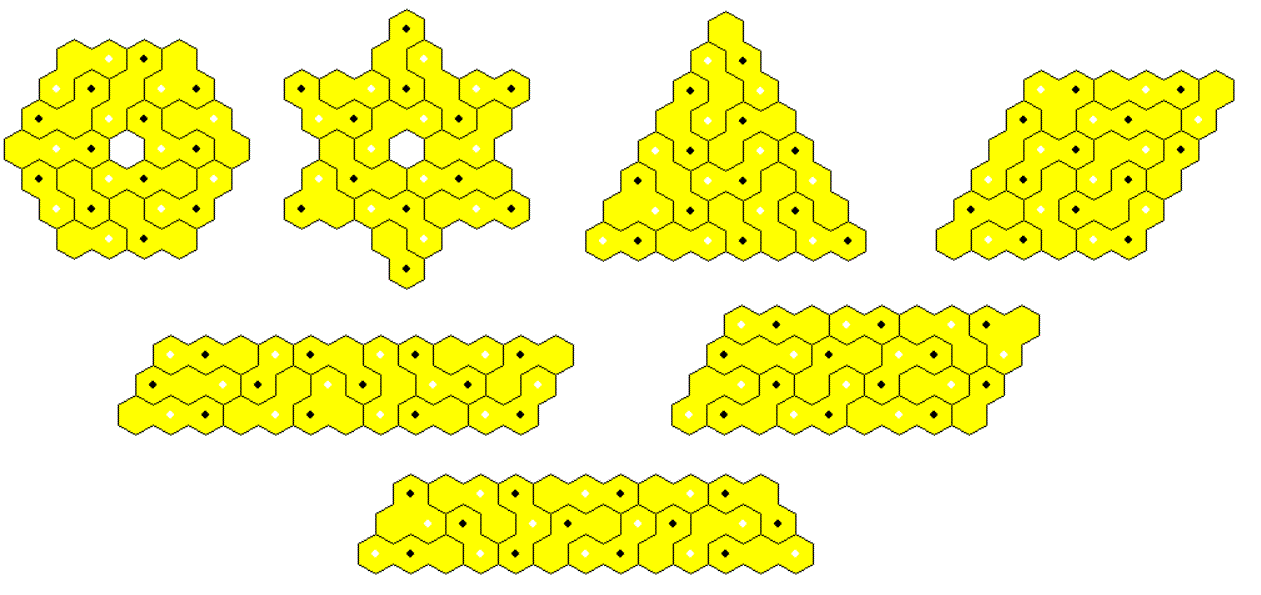
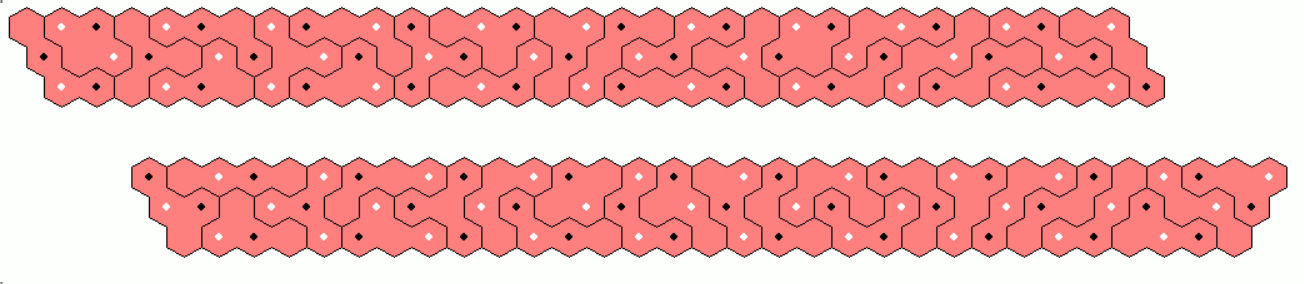
One-sided Trihexes, 11 Pieces
If we turn the two-sided pieces upside down, the order of colors doesn't change for the straight and the arc shaped pieces. Only the triangle shaped piece changes the order of colors and therefore we have a second piece of this type in the one-sided set.
Some figures with different symmetries are shown.
If we take a triangle of size 8 and remove a triangle of size 2, we get a similar hole figur; but unfortunately the hole cannot be placed at the center.
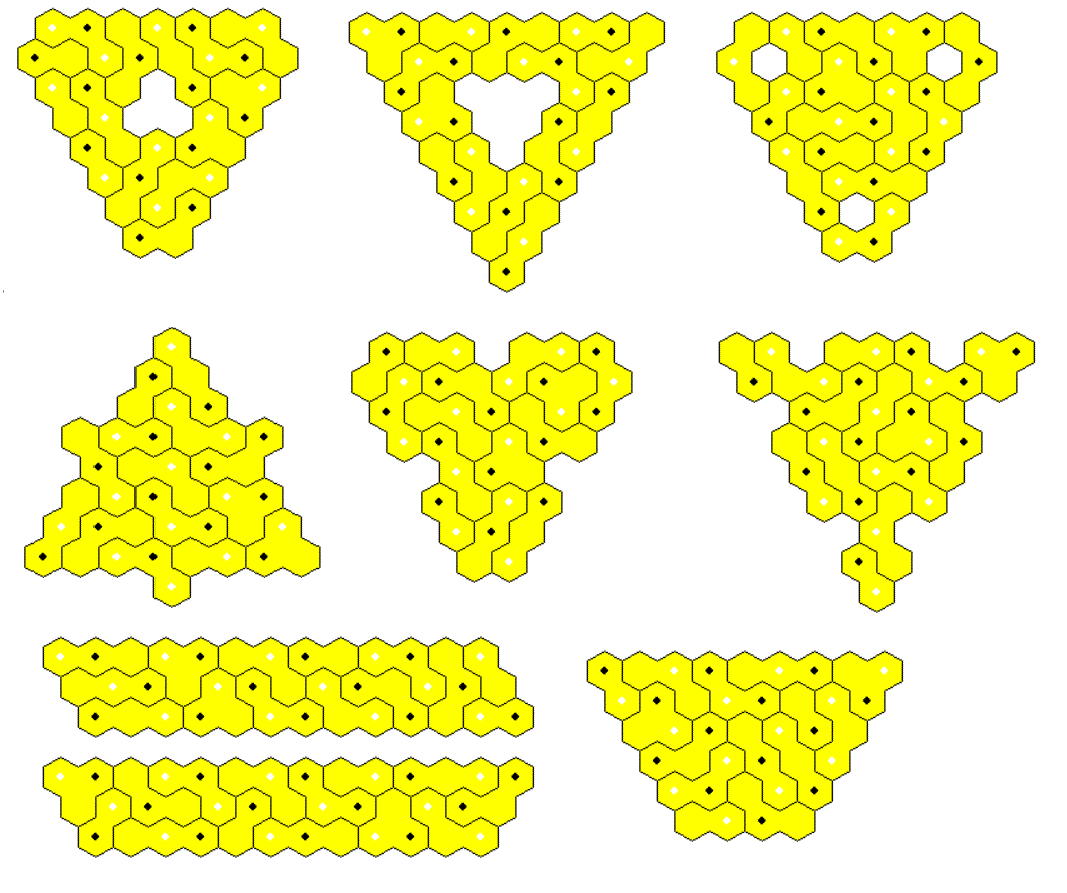
Two-sided Trihexes and Dihexes, 13 Pieces
Adding the 3 dihexes to the set of two-sided trihexes we get a total area of 36 hexagons which allows for figures with hexagonal symmetry. Furthermore it seems to be easier to get constructions by hand.
One-sided Trihexes and Dihexes, 14 Pieces
This set has a total area of 39 hexagons, which made it possible to construct figures with triangle symmetry. You can start with a trigangle of size 8 or 9 and subtract or add hexagons at symmetric positions.
Two-sided Tetrahexes 30 Pieces
The set has a total of 120 hexagons just enough to construct a triangle of size 15, since 15*16/2=120.
Figures with two axes of symmetry are a rhomb and kind of a hexagon, each with center holes.
Factorising 120 leads to a lot of parallelograms: 40x3 (two parts 20x3), 30x4, 24x5, 20x6, 15x8 and 12x10.
At last I looked for trapezia of height 3 or 5. It's even possible to construct three trapezia of height 5 and with a baseline of 10 hexagons, which can be combined to get another solution for the long trapezium. You must rotate the left and right trapezia by 180° . The solution was found by dividing the whole set into 10 subset, so that the three elements of each subset only differ in a cyclic shift of colors. A solution for one trapezium with only one piece of each subset can easily be transformed into a solution for the other two trapezia.
What about constructions with hexagonal symmetry? The number of same colored hexagons in rings around the center is always a multiple of 3. Therefore 40 same colored hexagons of the set cannot be placed in a hexgonal figure. But discarding three pieces with together 4 same colored hexagons of each color allows such a construction.
One-sided Tetrahexes 48 Pieces
The set has a total area of 192 hexagons and I looked for solutions of a(a+1)/2-3b(b+1)/2=192 to get semiregular hexagons with triangle symmetry.
A hexagon symmetric under 180° rotation is also possible.
There are five parallograms: 64x3, 48x4, 32x6, 24x8 and 16x12. For the first and the second one we have two parts, that can be combined to get the whole ones; but it's not possible to join them to get the 32x6 or the 24x8 parallelogram, respectively. To get a solution the bad star pieces must be used rather early during the construction procedure.
Only one trapezium with a baseline of 65 and a height of 3 is possible to construct. As with the parallelograms of smaller height you have to use bad pieces earlier.
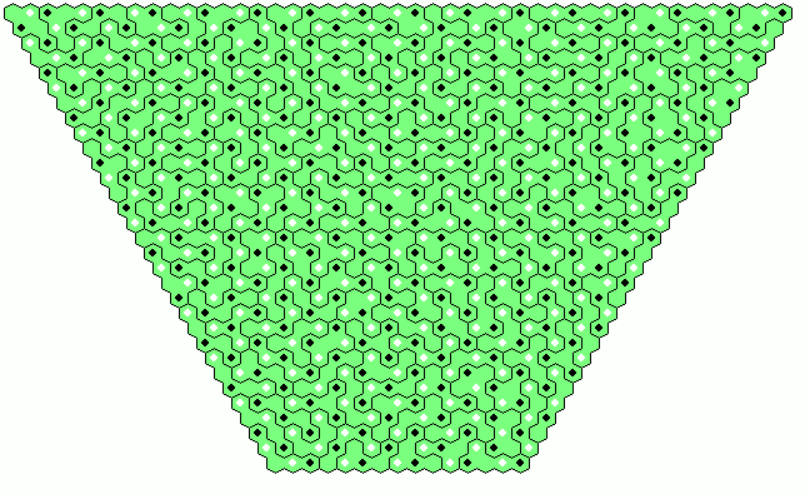
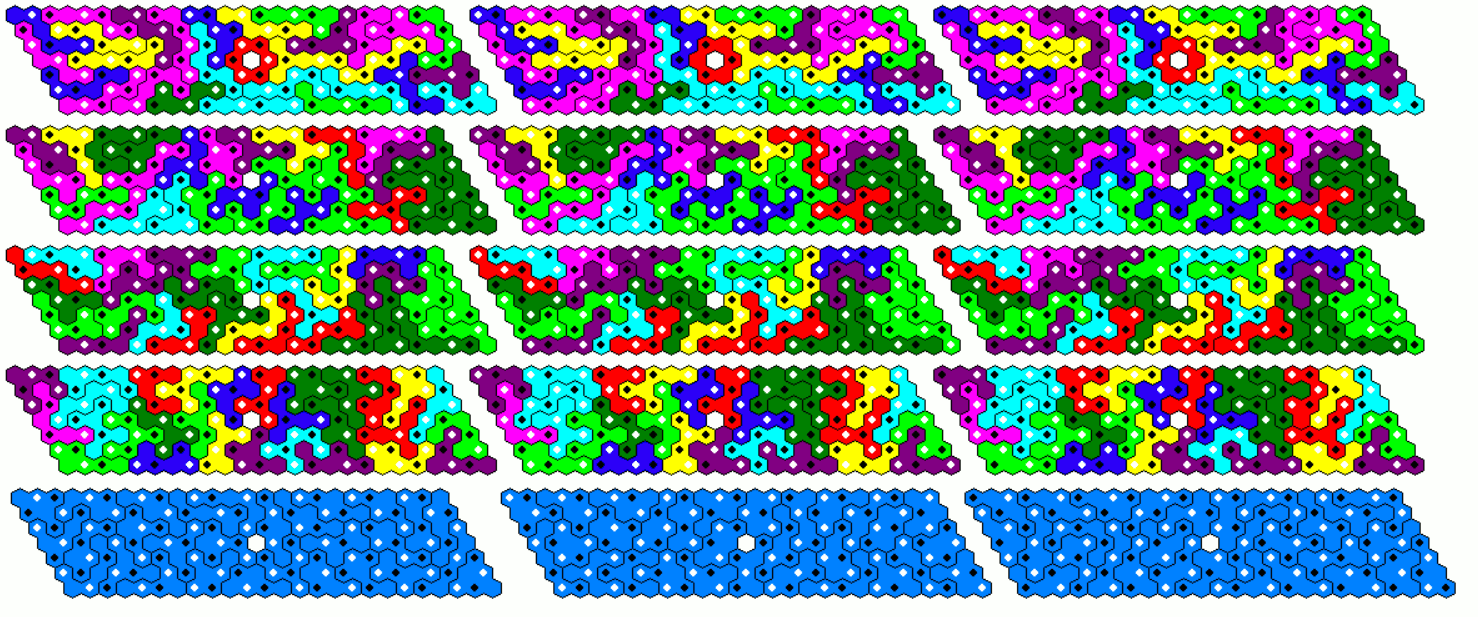
Two-sided Pentahexes 111 Pieces
Here is the set of pieces with a total of 555 hexagons. Beside the three colors of the grid, which are marked by black, white or missing dots in the center of the hexagons, some subsets of same colored pieces are shown to indicate that these three pieces only differ in a cyclic shift of the grid colors (white > black > empty > white). Dividing the whole set into 37 subsets allows multiple constructions, if you make a figur using only one piece of each subset and get two other ones by transformation.
Since 555=3*5*37 we can look for parallelograms of size 111x5 and 37x15. I made a 37x5 parallelogram and got two other ones by a cyclic shift of grid colors. Stacked on each other we get the 37x15 parallelogram whereas placed in a row we have the 111x5 parallelogram. The first part must be placed on the left, the third one in the center and the second one on the right to match the colors of the grid.
We can also construct trapezia of height 5, 6, 10, 15 and 30. For these figures the cycle method doesn't work and I split the whole figure into two or three parts, solved them and put them together. For the long trapezia with height 5 or 6 the parts are shown separately.
Here are the remaining trapezia.
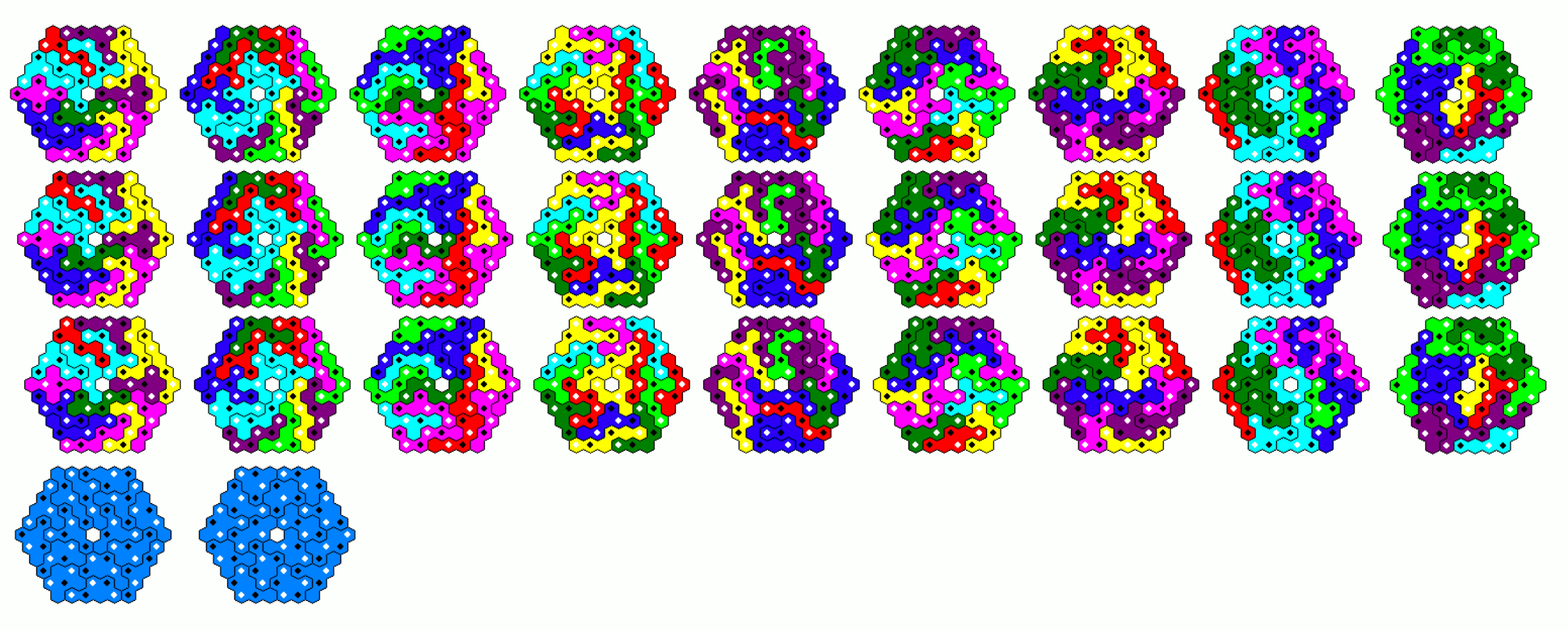
One-sided Pentahexes 111 Pieces
The set has a total of 930 hexagons. The only possible semiregular hexagon is a figure with side lengths of 12 and 25.
Since 930=2*3*5*31 we can try to construct a lot of parallelograms with this set. I made six parallelograms of size 31x5. Combining 1+2, 3+4 and 5+6 in a row we have three parallelograms of size 62x5. They can be stacked to get a 62x15 parallelogram or they can be joined for an even larger row of size 186x5. If we stack 1+4, 2+5 and 3+6, we have three parallolograms of size 31x10. They can be combined to get the 93x10 and the 31x30 parallelograms.
It's even possible to construct three trapezia with parallel sides of 25 and 6 hexagons using the color cycle method, but they doesn't fit together to get a trapezium with parallel sides of 56 and 37 and a height of 20. All possible trapezia with heights of 12, 15 , 20 and 30 are shown below.
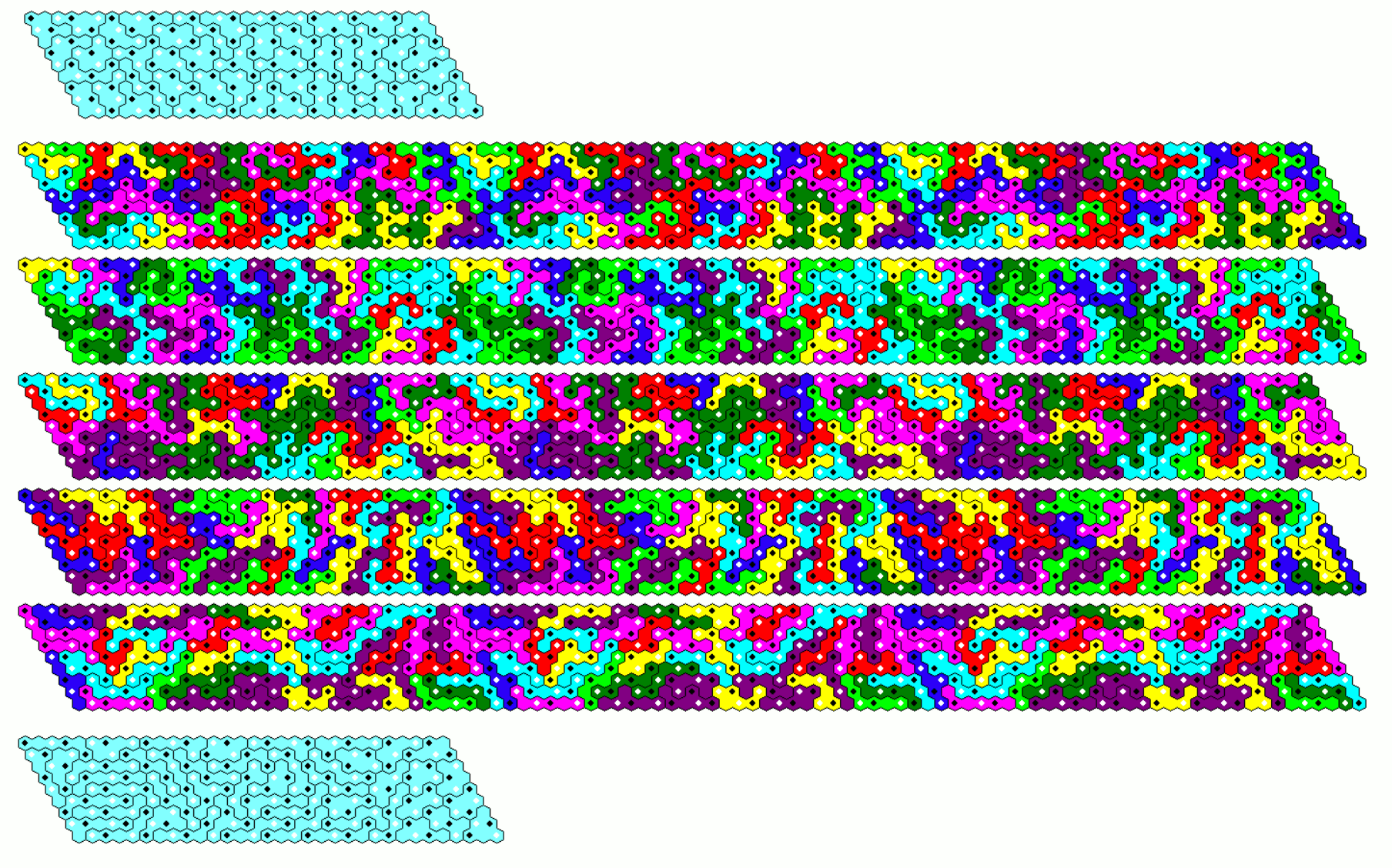
Two-sided Hexahexes 435 Pieces
There are three pieces with a hole, so that constructions without holes must leave out these pieces and we get a total area of 432*6=2592 hexagons. Since 2592=18*144, I looked for 18 rhombs of side length 12. Choosing subsets of three pieces each, which only differ in a cyclic shift of grid colors we have enough subsets to construct 5 rhombs with only one piece of each subset. With grid color transform we get 10 additional rhombs. Beside the grid colors black and white pieces of same shape are same colored to show the equal composition. The remaining pieces can be used to finish the construction of the last three rhombs.
Constructing 6 rhombs and adding 12 rhombs with a cyclic color shift isn't possible because there are three pieces, which don't change under the shift.
With the same method we can also get 15+3=18 parallelograms of size 18x8.
If constructions with holes are allowed, we have a total area of 435*6=2610. Factorising 2610=2*3*3*5*29 you can look for 15 parallelograms of size 25x7 with a hole at the center and an area of 25*7-1=175-1=29*6.
Hexagons with side length 6 and a center hole have a total area of 90. Therefore 29 hexagons of this size migth be possible to make with the set. Here is a solution with nine sets of 3 hexagons each and two single ones.
One-sided Hexahexes 816 Pieces
We have 813 pieces without holes and a total area of 813*6=4878=2*9*271. The following six pieces are invariant under cyclic color shift.
The other ones can be combined in subsets of three pieces, where the pieces only differ in a cyclic grid color shift. With these pieces we can make five parallelograms of size 32x9 using only one piece of each subset. Then we get 10 additional parallelograms by color transformation. Joining the parallelgrams with their transformed ones we have five parallelgrams of size 96x9. With the remaining pieces we can fill parallelograms of size 32x9 and 30x9 to get a large parallelogram of size (5*96+32+30)x9=542x9.
A semiregular hexagon with side lengths of 59 and 25 can also be constructed with the pieces. I divided the whole area into six parallelograms of size 95x12 and a triangle of side length 35. After the parallelograms were easily found by the cyclic color shift method, I had to split the triangle into three parts to finish the construction.
If we also use the three pieces with holes we have a total area of 816*6=4896. This allows a multiple construction of 17 rhombs with a center hole and side lengths of 17.
Home