Bridged Polyspheres

2018/08/02

Polyspheres are made of touching spheres in the face centered cubic lattice. You can see some construction with these pieces on the polysphere section of my site. Since there are holes between the spheres small sticks or bridges can be used to connect spheres which have a distance of sqrt(2)*2r between their centers. If these connections are allowed, you can get much more different pieces with a fixed number of spheres. Jared McComb came up with this idea and I changed my computer program for polyspheres to create these bridged polyspheres. There are two difficulties.

Modelling the spheres as little cubes, which can only be turned around the three coordinate axes, you have to look for those pieces, which are different if made from cubes but identical if made from spheres.

If you have pieces with four or more spheres and the position of the spheres is set, you can somtimes choose the position of the bridges in different ways. To avoid pieces with parts connected by more than one bridge the bridges must produce a span tree with ordinary polyspheres as leaves.

After I had created the pieces I looked for some symmetric constructions.

Unfortunately the program sometimes produced solutions with interlocking pieces and a physical construction wasn't possible. Sometimes it only seemed to be impossible to insert the next piece into a partly assembled construction, but when the construction was pulled apart at least a little bit, you could insert the piece and fill an existing hole. Therefore I glued all pieces with up to 4 spheres from ping pong balls and little plastic tubes using a hot glue gun. With a jig I got the precise distances and angles. This way I could check the computer solutions. Sometimes this check failed and I had to start with a new computer solution.
Here are all pieces with one to three spheres.

In the face centered cubic lattice we have planes with hexagonal grid structure and planes with square or orthogonal grid structure. I used three kinds of bottom layers for my constructions.

Equilateral triangles in the hexagonal grid with n touching spheres at each side.
Now tetrahedrons with n*(n+1)*(n+2)/6 spheres can be constructed.
Compact rectangles in the orthogonal grid touched by m or n spheres at their sides.
For n=m you can get square pyramids with n*n + (n-1)(n-1) + ... + 1=n(n+1)(2n+1)/6 spheres.
For n < m roofs with a bottom layers of n*m and a total of n(n+1)(2n+1)/6+n(n+1)/2*(m-n) spheres are possible.
Pedestals or dams can be made if k top layers of a roof are removed.
Kind of jagged rectangles touched by a and b spheres at their sides but with gaps between the spheres.
So we can stack c layers with a*b+(a-1)(b-1) and c-1 layers with (a-1)*b+a*(b-1) spheres which gives a box with c*(2a-1)(2b-1)-((2a-1)(2b-1-1)/2 spheres.

The following table lists some sets or subsets of bridged polyspheres and constructions, which can be made with them. Click the sets to see the pictures and computer solutions.

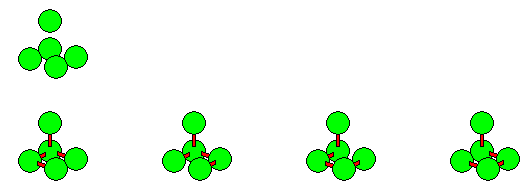
Number of Spheres	Special Properties	Number of Pieces	Total Volume	Constructions
1	-	1	1	-
2	-	2	4	-
3	-	9	24	beveled box
1 or 2	-	3	5	square pyramid
1 or 3	-	9	25	rectangular or octogonal pedestal
2 or 3	-	10	28	two pyramids, roof
1 to 3	-	11	29	pedestal, octogonal basin
4	flat in the orthogonal grid	22	88	flat figures, box
4	flat	35	140	square pyramid, roof, dam
4	nonflat	51	204	square pyramid, 2 tetrahedrons, triangle dipyramid
4	-	86	344	octahedron, dam. terahedrons
3 or 4	-	94	368	boxes, terahedrons, dam
5	-	1149	5745	-

Home