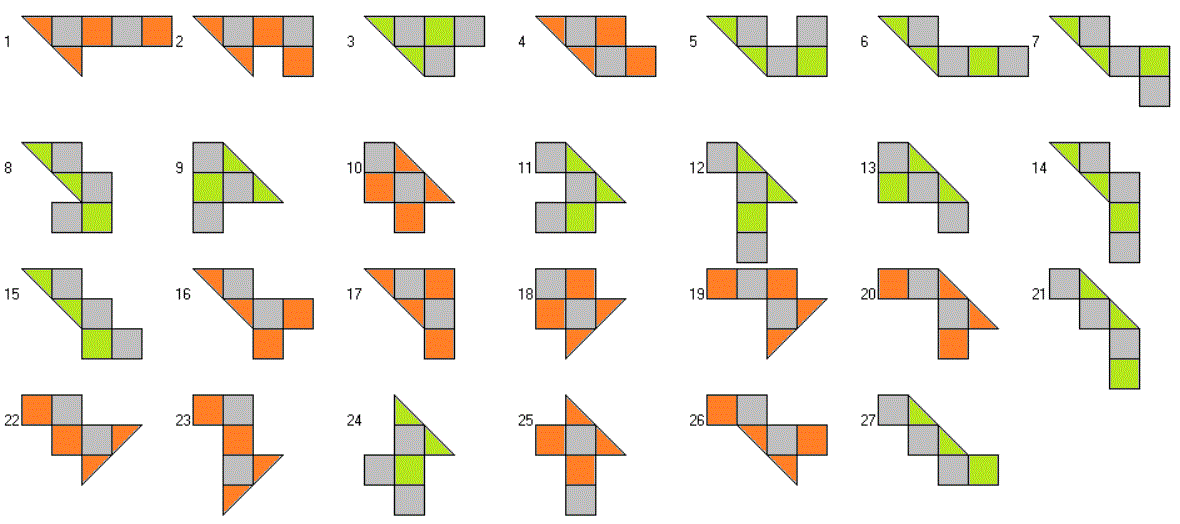Big Tan plus Squares

2023/10/31
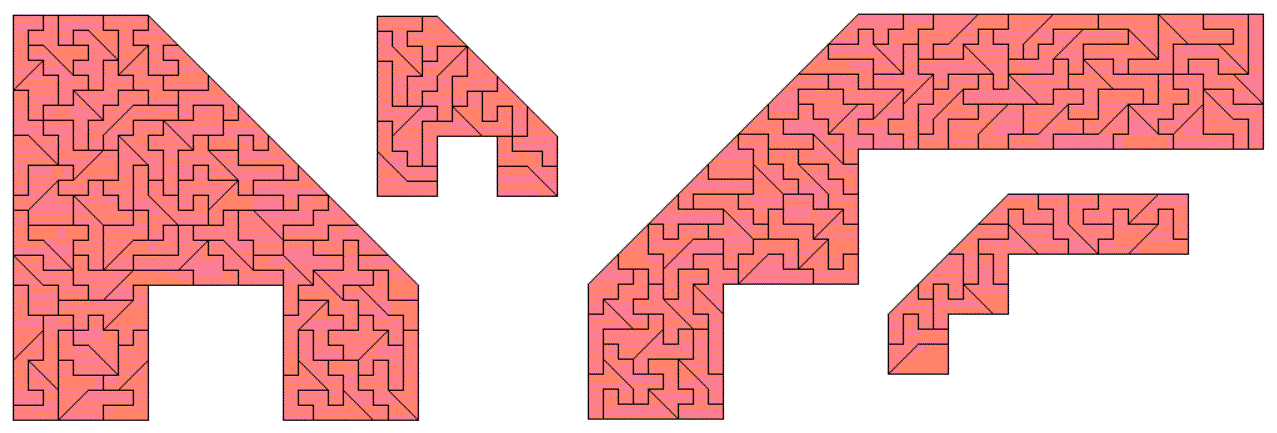
Take a 2x2 square from an orthogonal grid and slice it diagonally. To this triangle called big tan you can add N squares to get different pieces. As shown above all 27 pieces with three additional squares can be used to fill a rectangle of size 13x10 with one piece left. A rectangle with no pieces left isn't possible because the number of pieces is odd and the sliced edges must touch each other. But you can get convex and symmetric figures with this set like the following one.

You may also start with a polyomino made from N+4 squares and try to cut a big tan with one cut so that the piece doesn't fall apart. This way you get a slightly smaller set, where all pieces with an inner angle of 315° are missing.

Click the different sets in the table to see construction with them. Sometimes there are conditions, which prevent a solution.

Two-sided Pieces One-sided Pieces
Number of Squares Additional Property Number of Pieces Area Number of Pieces Area
2 - 8 32 14 56
3 - 27 135 53 265
no 315° angles 26 198 51 396
4 - 105 630 206 1236
no 315° angles 97 582 190 1140

Big Tan plus 2 Squares, 8 Two-sided Pieces

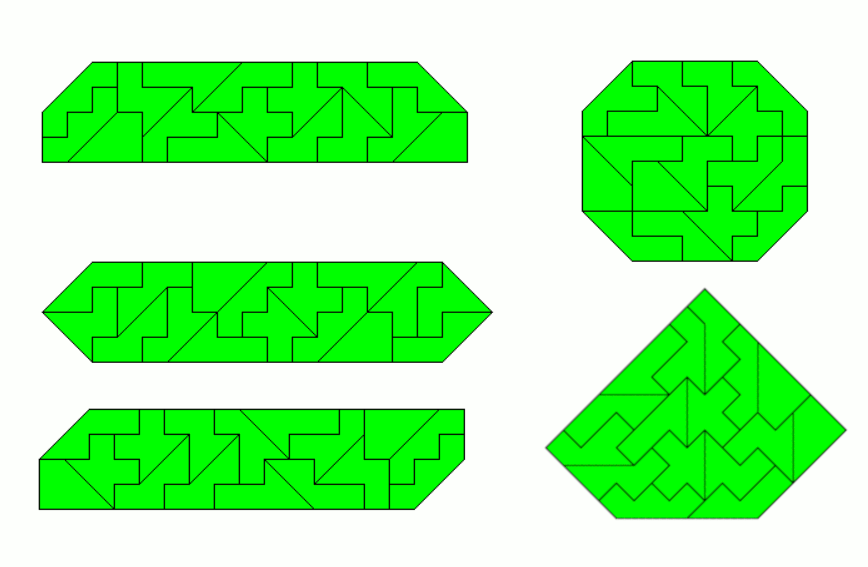
The two-sided set has only 8 pieces with a total area of 32 square units. Unfortunately a 8x4 rectanglecan't be packed with these pieces, but at least two figures with one axis of symmetry are possible to construct.

You can take two sets of these pieces with an area of 64 square units, but there is no chance to make a rectangle with these pieces. After all I got a pentagon, an octagon and three symmetric hexagons.

Big Tan plus 2 Squares, 14 One-sided Pieces

There are two symmetric pieces in the two-sided set. Therefore we get (8-2)*2 + 2 = 14 pieces with a total area of 56 square units. Once more the construction of rectangles failed, but some convex figures with one axis of symmetry can be made.

Rotational symmetry is also possible.

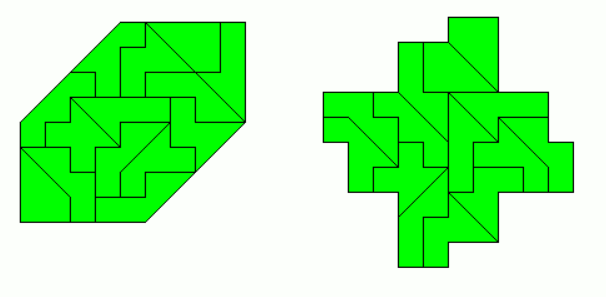
If the figures don't have to be convex, you can get further constructions with up to two axes of symmetry.

Big Tan plus 3 Squares, 27 Two-sided Pieces

Here are the 27 pieces with three additional squares and a total area of 135 square units. Under checkerboard coloring 1 or 2 of the additional squares get the same color as the sliced squares of the big tan. Let's call them P1 or P2 pieces, respectively. Then we have 14 P1 pieces, which are green marked and 13 P2 pieces, which are brown marked.

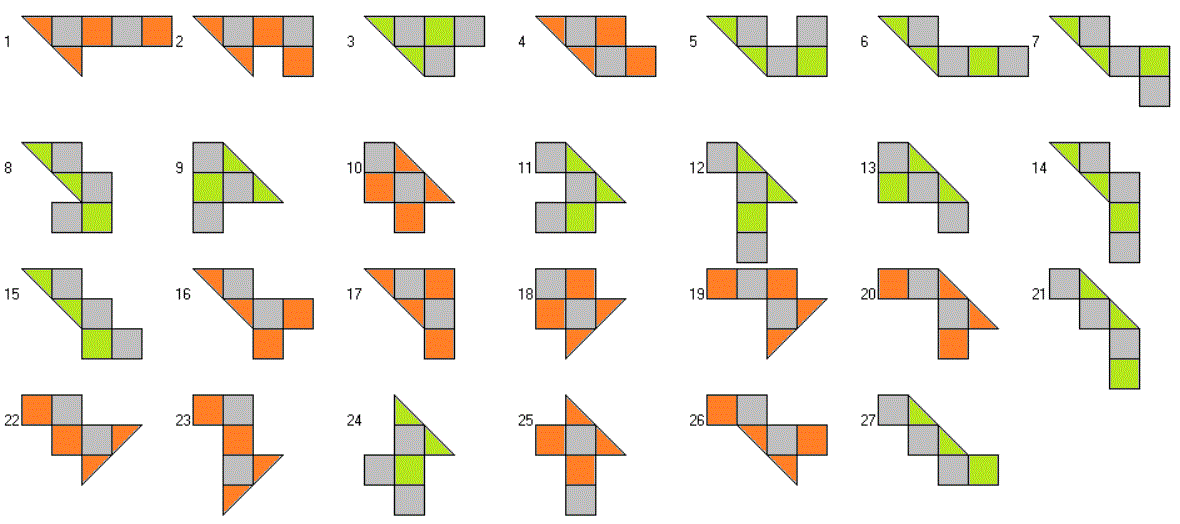
Since a rectangle with all pieces can't be constructed because of the odd number of sliced edges I tried to make 13x10 rectangles with one piece left. This piece must be a P2 piece. Let d be the difference between white and black squares under checkerboard coloring we have:

If m is the number of mixed pairs P1-P2 in the rectangle, there are 14-m=r and 13-m=r-1 remaining pieces for the other pairs; r can't be even because we would have r/2 P1-P1 pairs and (r-2)/2 P2-P2 pairs together (r+r-2)/2=r-1 and an odd number of those pairs can't balance the number of black and white squares. With an odd r we get (r-1)/2 P1-P1 pairs and (r-1)/2 P2-P2 pairs with one P1 piece left.

One example is shown, a second one is in the title and the other ones are here.

If you allow a second copy of one P2 piece, you can also construct a 14x10 rectangle, where a hole in the rectangle can be filled with the additional piece. An example is shown, the other ones are here.

We can also slice rectangles at their corners to get figures, which can be packed with the complete set.

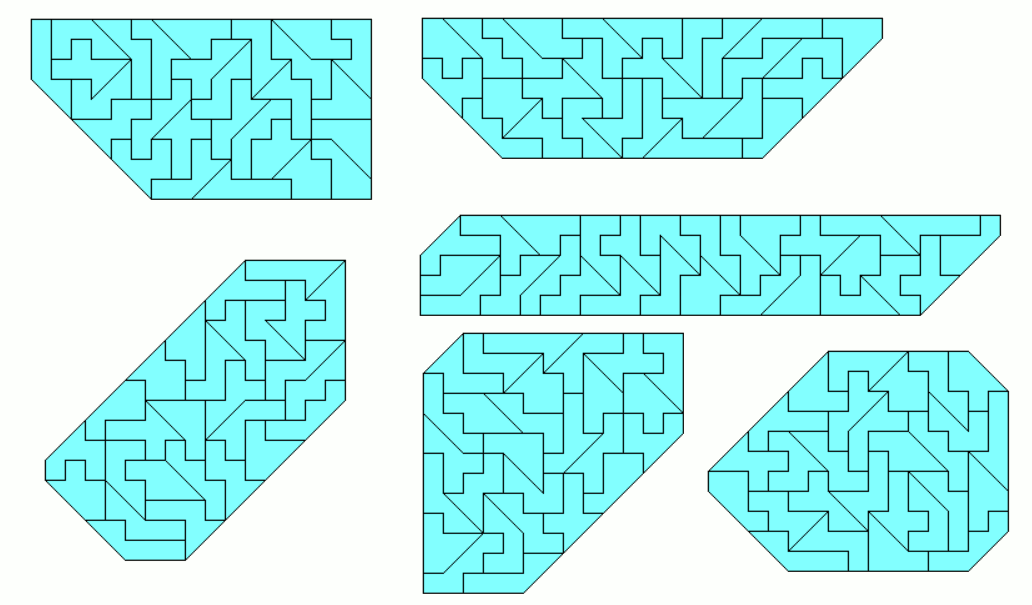
Big Tan plus 3 Squares, 53 One-sided Pieces

Since there is only one symmetric piece in the two-sided set we get 26*2+1 = 53 one-sided pieces with a total area of 265 unit squares. Using the definition for the two-sided pieces we have 28 P1 pieces and 25 P2 pieces. At first I tried to construct a 21x15 rectangle, where an isosceles, rectangular triangle with legs of size 10 was removed. But this failed.

The total area of the figure can get a checkerboard coloring with a black to white ration of 233:232, if the sliced side is white. Let m be the number of pairs, which consist of a P1 and a P2 pieces connected at their sliced sides or both located at the sliced side of the figure. These pairs are balanced and cover an area of 5m+5m=10m. The numbers of remaining pieces are 28-m=r+3 and 25-m=r for the P1 and P2 pieces, respectively.

We can discuss two cases:

You can neither construct other sliced rectangles, because the sliced parts have an even area and the sliced rectangles have an unbalanced number of black and white squares.

What about replicas of the pieces? We can look for a 2-fold plus a 7-fold copy of them, because 2*2+7*7=53. For some pieces you can't get 2-fold copies and the 7-fold copy failed for P1 pieces, because the black and white difference is 1. For P2 pieces the differenc is 2 and a construction is possible. One example is shown, the other ones without the reflected solutions are here.

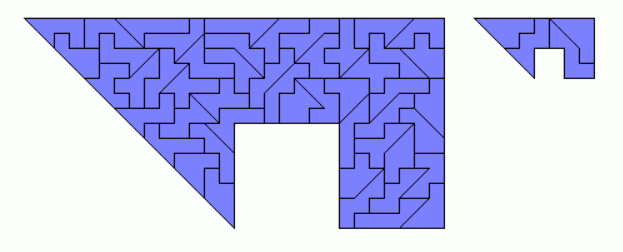
Heptominoes with Big Tans Cut off, 26 Two-sided Pieces

Look at the 27 pieces made from one big tan with three additional squares. All but one (nr. 8) can be made by taking a heptomino and cut off a big tan by a single cut. Now the number of sliced edges is even and we can construct two rectangles of size 13x10 and 26x5 with the whole set, which has a total area of 130.

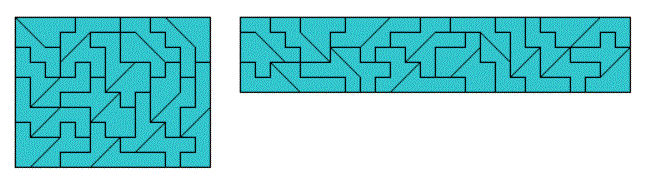
Other symmetric figures and sliced rectangles are also possible.

Then I made some 5-fold replicas of the pieces using 25 pieces of the set. Unfortunately the left piece can't be the replicated one. One example is shown the other ones are here.

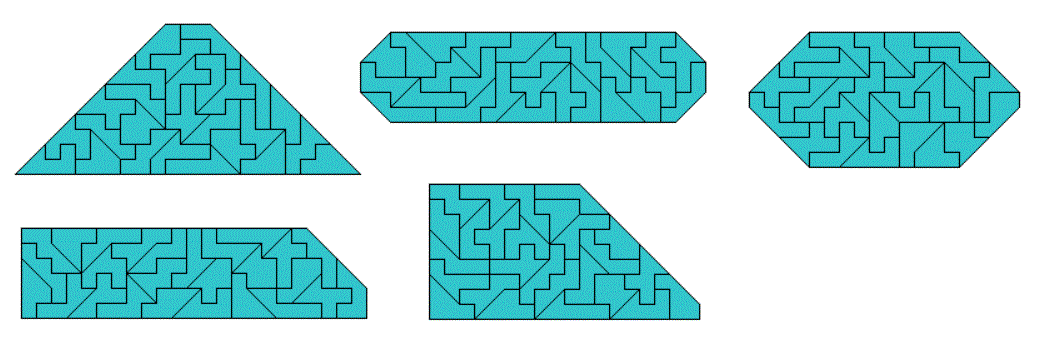
Heptominoes with Big Tans Cut off, 51 One-sided Pieces

Here are the printed pieces. Since there is only one symmetric piece in the two-sided set, we have (26-1)*2+1=51 pieces with a total area of 255 square units.

Because of the odd number of sliced edges rectangles can't be made, but some symmetric constructions are possible. You can take 19x19 squares and cut off two or four corners.

Starting with an 18x18 square is also possible.

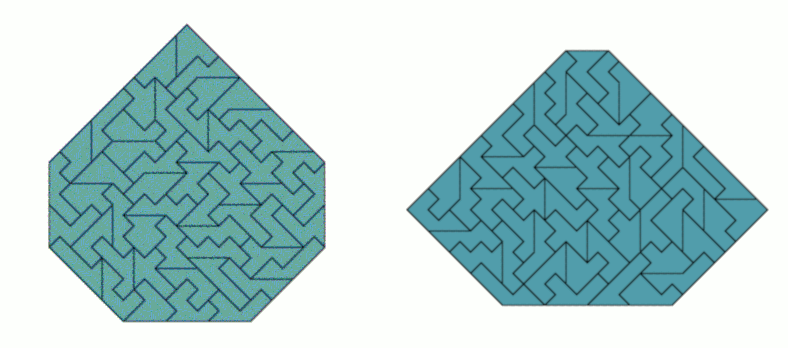
We can also get convex polygons with 5, 6 or 8 corners.

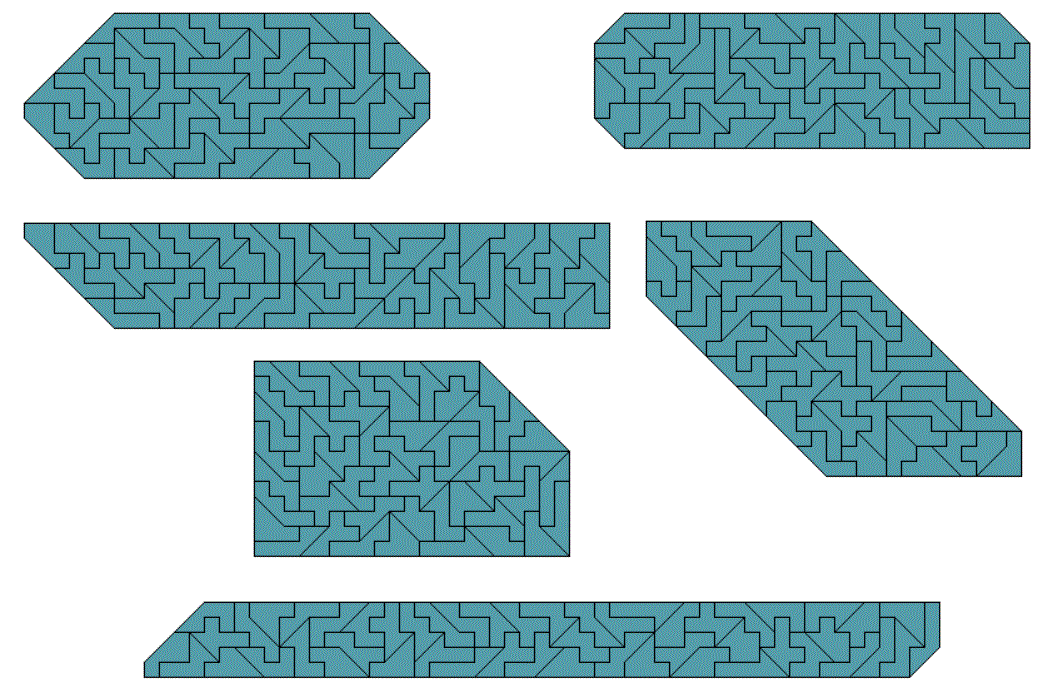
Big Tan plus 4 Squares, 105 Two-sided Pieces

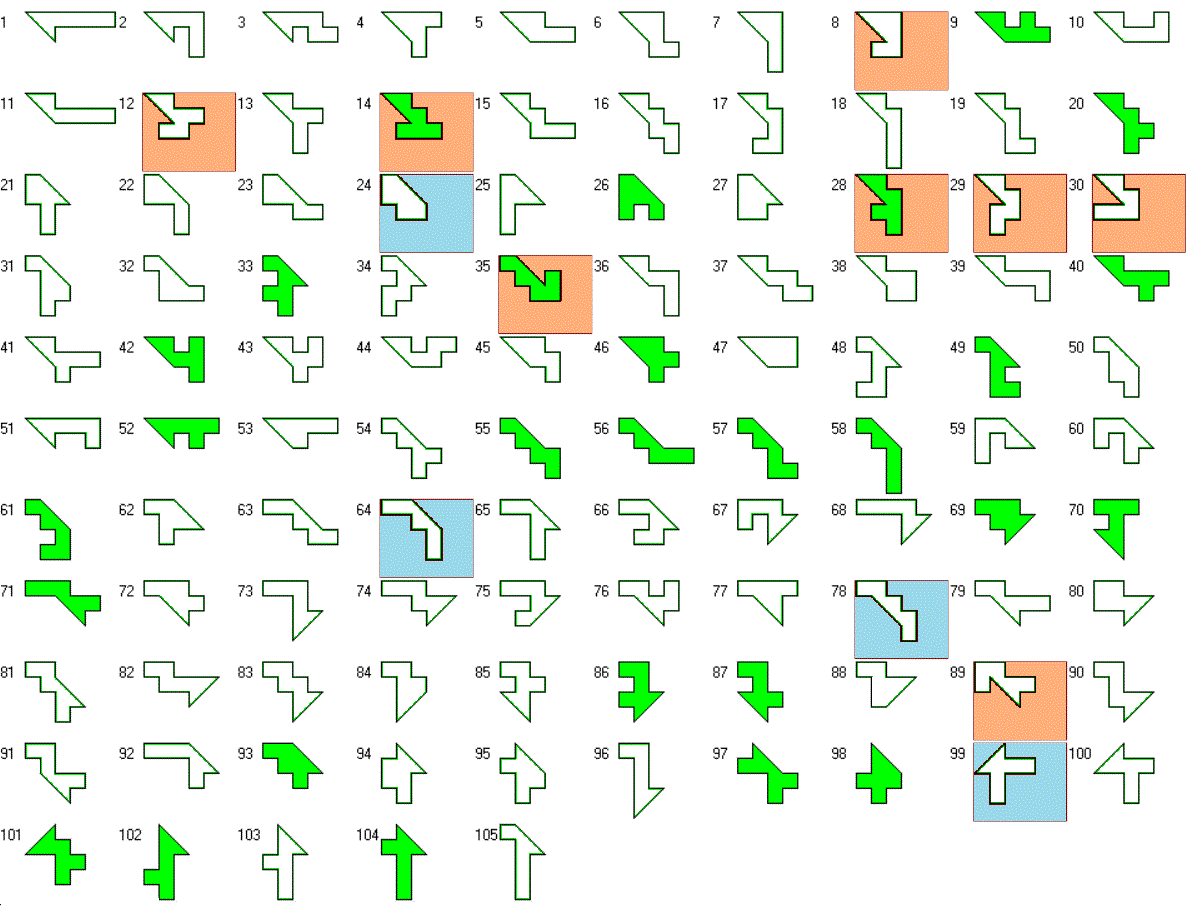
Here are the 105 pieces 77 of them are balanced and 28 are unbalanced under checkerboard coloring. The unbalanced pieces are green colored, the symmetric pieces have a blue background and the pieces, that can't be derived by cutting an octamino, have a red background.

You cannot construct any rectangle, because the number of pieces is odd; but sliced rectangles are possible.

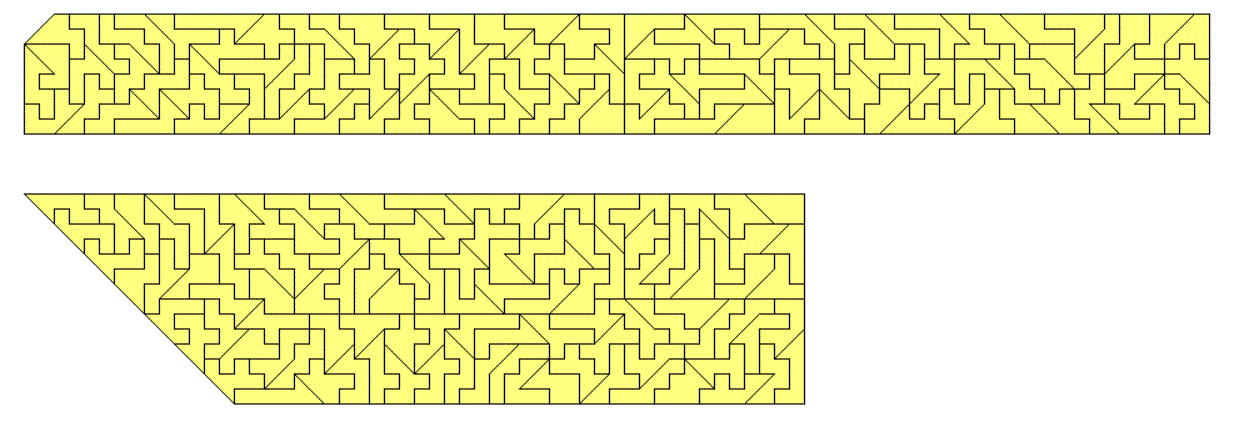
You can also look for rectangles with holes shaped like replicas of the pieces. Two examples for a 30x26 rectangle with a hole like a 5-fold copy of a piece is shown.

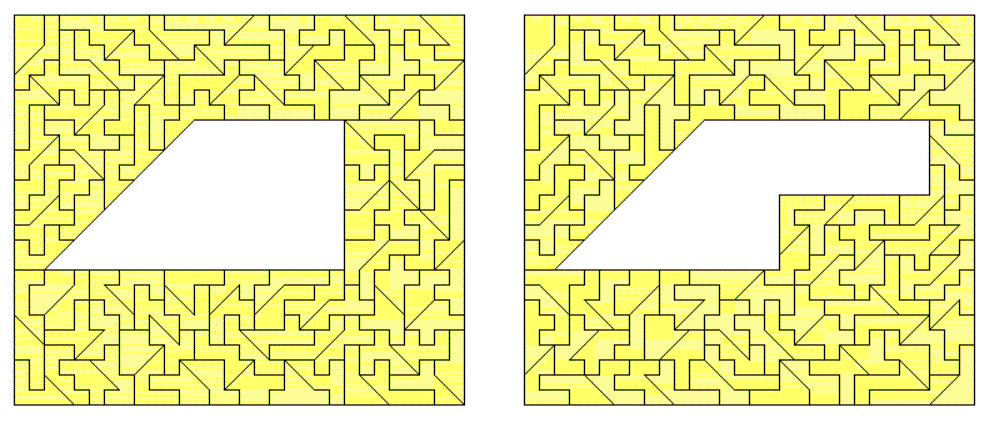
Rectangle of size 30x22 with two holes shaped like a piece and its 2-fold copy might be possible for some pieces.

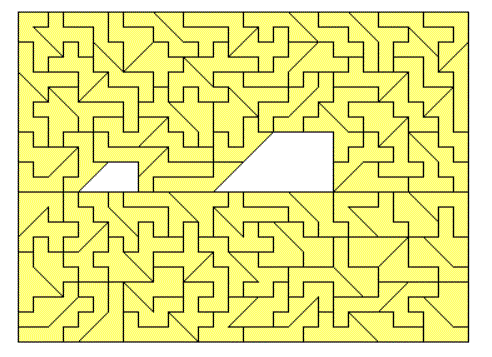
Here are three simultaneous 4-fold, 5-fold and 8-fold replicas of one piece. Since 16+25+64=105 all pieces are used.

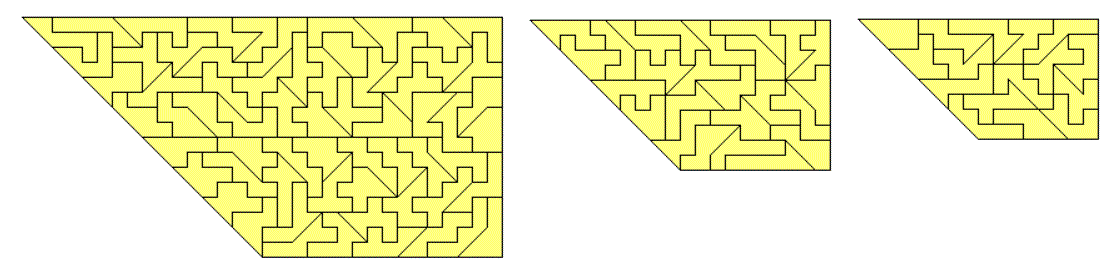
At last you might look for some similar hole figures, where a 7-fold hole of a piece is placed in its 11-fold copy.

Big Tan plus 4 Squares, 206 One-sided Pieces

We have (105-4)*2+4=206 one-sided pieces. This is an even number of pieces and among them are an even number of balanced pieces. Therefore we can look for rectangles with an area of 1263=103*3*2*2. The 103x12 rectangle is shown, but the 203x6 rectangle seems to be very hard to construct, if possible at all.

We can also get rectangles with one or more sliced corners. Here is an example with two axes of symmetry.

What about multiple replicas of the pieces? I constructed a 6-fold and a 13-fold replica of one piece without using it. Then 1²+6²+13²=205.

Octominoes with Big Tans Cut off, 97 Two-sided Pieces

Since the total number of pieces is odd rectangles made from all pieces are impossible. With one piece left a lot of rectangles can be constructed because the reduced area is 96*6 = 576 = 2*2*2*2*2*2*3*3.

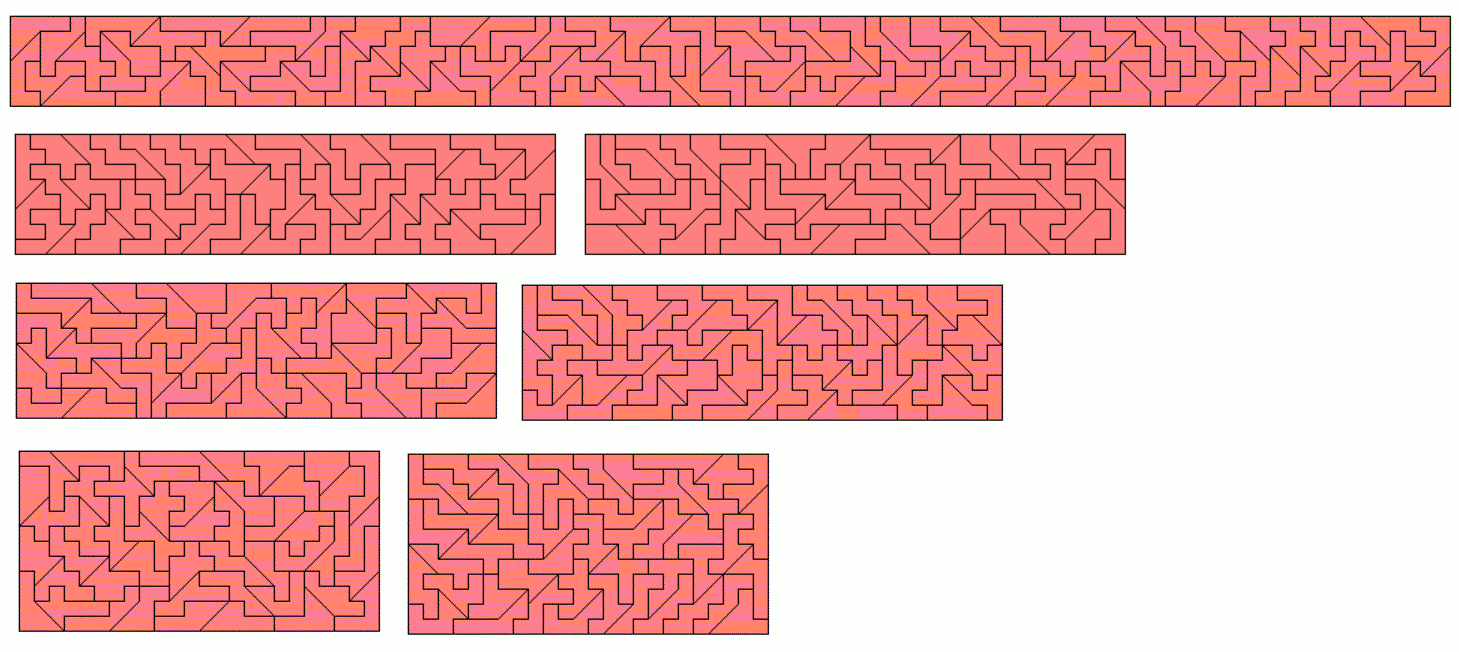
With one piece left a quadratic ring of size 26² - 10² can also be constructed.

I furthermore looked for combined replicas of the pieces because 97 = 81+16. In this case you can only choose unbalanced pieces, because the whole set has an odd number of unbalanced pieces and the 9-fold copy is only unbalanced, if the replicated piece is unbalanced.

Octominoes with Big Tans Cut off, 190 One-sided Pieces

There are (97-4)*2+4=190 one-sided pieces with a total area of 1140. Since the number of pieces and the number of unbalanced pieces are even, rectangles can be constructed: 95x12, 76x15, 57x20 and 38x30. A solution for a 190x6 rectangle seems to b hard to get, if possible at all.

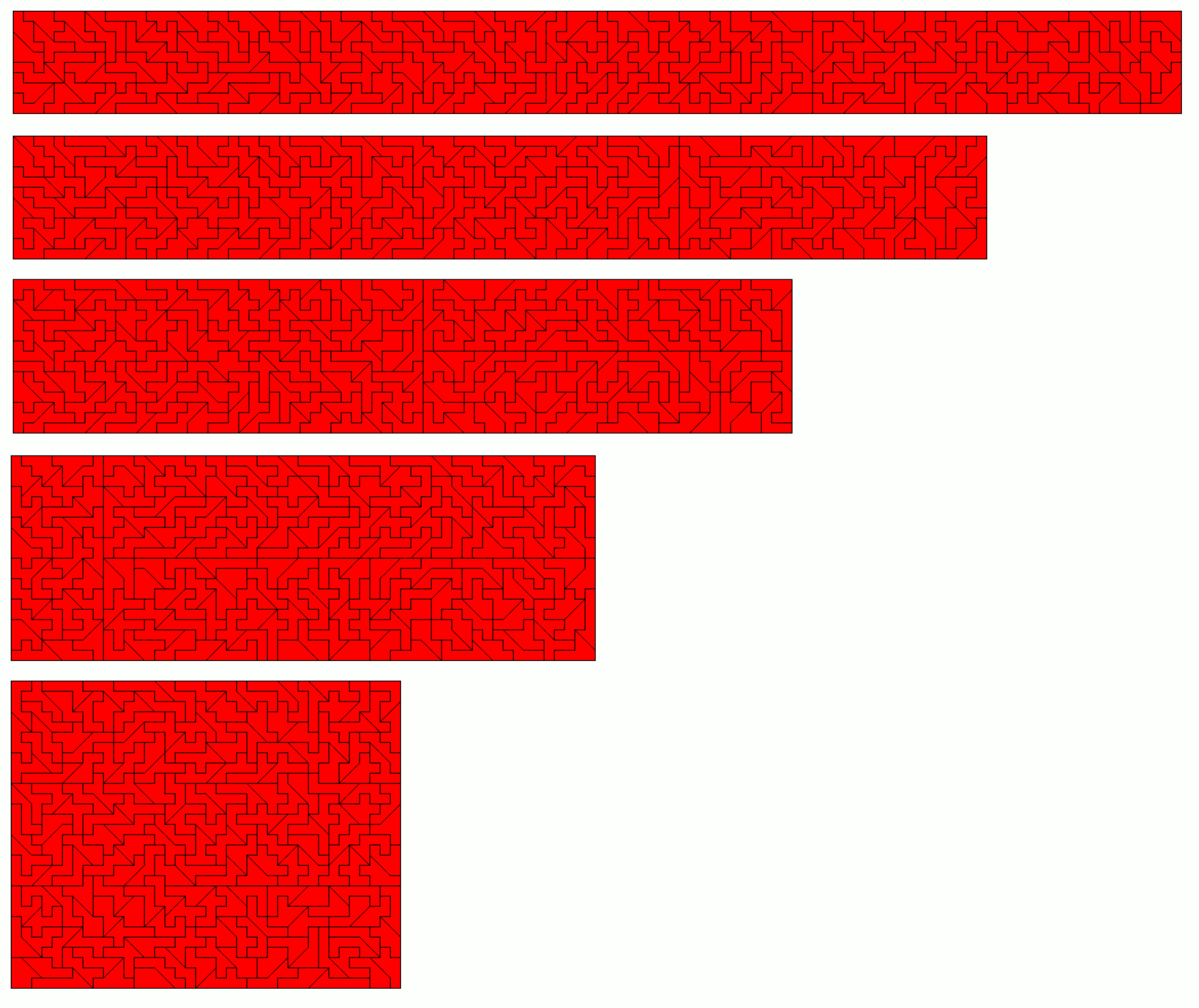
Instead I constructed simultaneous 3-fold, 9-fold and 10-fold replicas of two pieces, because 3²+9²+10²=190.

We can also get rectangles with one or more sliced corners. Here is an example with two axes of symmetry.

Home