Archimedean Solids Covered with Matching Polygons

2023/01/24
Beside the Platonic solids the Archimedean solids are convex solids with regular faces and an identical structure of their vertices. I tried to use polygons with colored sides to cover the solids so that same colored sides match at the edges of the solid. Given a fixed number of colors there are often too few or too many different polygons to cover the faces of a single Archimedean solid. Therefore some polygons must be used more than once, or some pieces with special properties must be discarded.

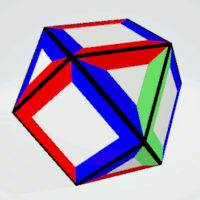
It's also possible to add kind of folds and gaps at these folds to connect the polygons by U-clips. The positions for the gaps are: center (0), right from center (1), left from center (-1), far right from center (2) and far left from center (-2). A gap x then matches a gap -x. At the virtual objects the center positions are always red marked, left and right positions are blue marked and the more distant positions are green marked. In this case the folds must lie in a plane defined by two corners of the polygon and the center of the solid. Above you can see a printed version of such a rhombicosidodecahedron.

For the Archimedean solids with more than 30 faces you should use a suitable order to place the polygons onto the solid. For instance you can sort the faces due to the height of their centers of gravity.

For the printed versions I also took solid polygons.


Click the pictures in the table to see examples of covered Archimedean solids and the used sets of polygons. If you click these examples you can also see virtual models of them.


Icosidodecahedron
20 Triangles
12 Pentagons
Truncated Cube
8 Triangles
6 Octagons
Snub Cube
32 Triangles
6 Squares
Truncated Cuboctahedron
12 Squares
8 Hexagons
6 Octagons
Truncated Octahedron
6 Squares 8 Hexagons

Rhombicosidodecahedron
20 Triangles
30 Squares
12 Pentagons
Cuboctahedron
8 Triangles
6 Squares
Rhombicuboctahedron
8 Triangles
18 Squares

Truncated Icosidodecahedron
30 Squares
20 Hexagons
12 Decagons
Truncated Icosahedron
12 Pentagons
20 Hexagons
Snub Dodecahedron
80 Triangles
12 Pentagons
Truncated Dodecahedron
20 Triangles
12 Decagons
Truncated Tetrahedron
4 Triangles
4 Hexagons

Cuboctahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
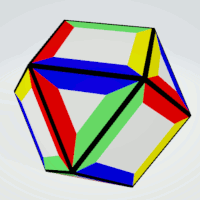Squares 4 all sides must be different 6 1 6
Triangles 4 all sided must be different 8 1 8
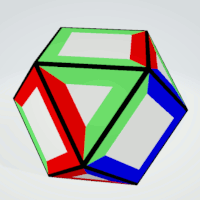Squares 3 three equal sides,
one different side		 6 1 6
Triangles 3 all sides must not be equal 8 1 8
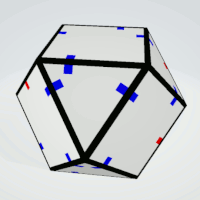
Squares 3 two pairs of equal sides 6 1 6
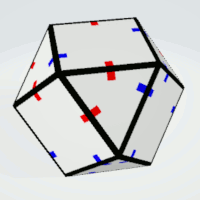Triangles3 all sides must not be equal 8 1 8

That's a real construction with colors. You can start with the net for the solid and put the magnetic polygons on an iron surface.

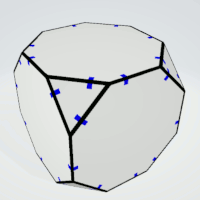
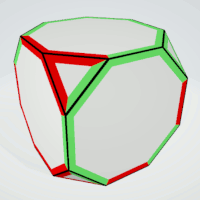
Truncated Cube

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
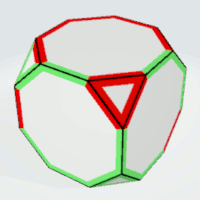Octgons 2 exactly two equal sides
not neighboring		 6 1 6
Triangles 2 - 4 2 8
Octagons 2 exactly two equal sides
not opposite		 6 1 6
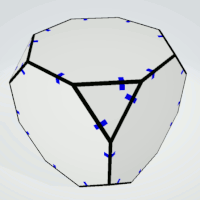Triangles 2 - 4 2 8

In the printed version all triangles have a gap at the center of their sides. The octagons have also center gaps at four sides but between these sides the other ones have gaps right or left from center. It's easy to arrange the octagons with matching gaps, and then you can finish the construction.

Truncated Icosahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
Hexagons 2 at least two sides of each kind 10 2 20
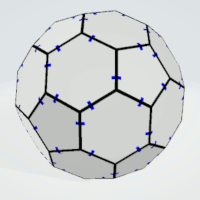Pentagons 2 all sides must not be equal 6 2 12
Hexagons 2 exactly three equal sides
aren't allowed		 10 2 20
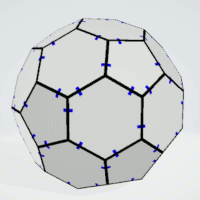Pentagons 2 all sides must not be equal 6 2 12

This is a real solid where the marks are replaced by gaps, and the polygons are connected at these points.

Icosidodecahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
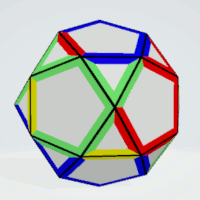Pentagons 4 exactly four equal sides 12 1 12
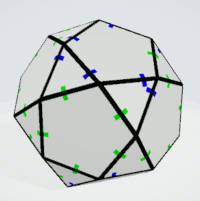Triangles 4 all sides must not be equal 20 1 20
Pentagons 2 all sides must not be equal 6 2 12
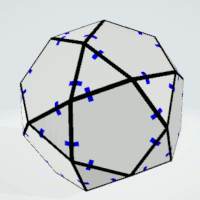Triangles 2 - 4 5 20

Here is the net and the finished construction of the solid.

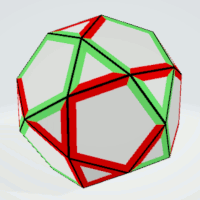
Rhombicuboctahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
Squares 4 all sides are different 6 3 18
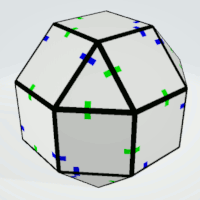Triangles 4 all sides are different 8 1 8
Squares 3 two pairs of equal sides 6 3
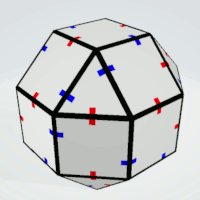Triangles 3 all sides must not be equal 8 1 8

Snub Cube

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
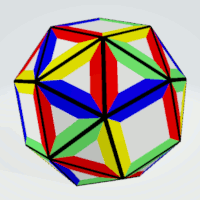Squares 4 all sides are different 6 1 6
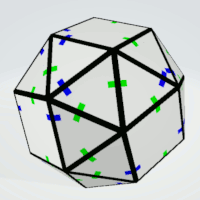Triangles 4 all sides are different 8 4 32
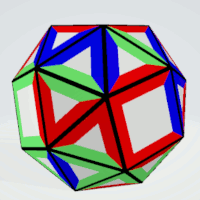Squares 3 exactly three sides are equal 6 1 6
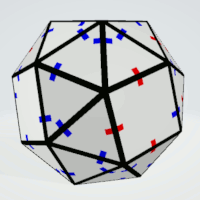Triangles 3 all sides must not be equal 8 4 32

Snub Dodecahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
Pentagons 2 all sides must not be equal 6 2 12
Triangles 3 all sides must not be equal 8 10 80
Pentagons 2 all sides must not be equal 6 2 12
Triangles 4 all sides must not be equal 20 4 80
Pentagons 2 all sides must not be equal 6 2 12
Triangles 4 all sides must be different 8 10 80
Pentagons 2 all sides must not be equal 6 2 12
Triangles 5 all sides must not be equal 40 2 80

If five colors are available for the triangles but only two for the pentagons it's necessary to keep track of the triangles with all colors different from the two colors for the pentagons. With these triangles only a restricted number of places can be covered.

Truncated Icosidodecahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
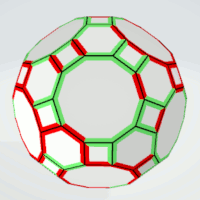Decagons 2 eight or nine equal sides 12 1 12
Hexagons 2 at least two sides of each kind 10 2 20
Squares 2 - 6 5 30

Rhombicosidecahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
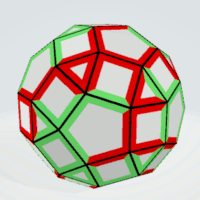Pentagons 2 all sides must not be equal 6 2 12
Squares 2 - 6 5 30
Triangles 2 - 4 5 20
Pentagons 4 exactly four equal sides 12 1 12
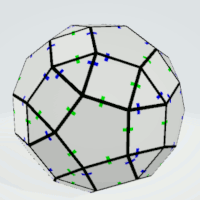Squares 4 all sides are different 6 5 30
Triangles 4 all sides must not be equal 20 1 20
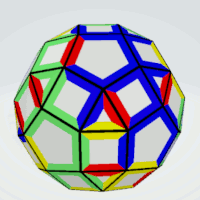Pentagons 4 exactly four equal sides 12 1 12
Squares 4 Two or four kinds of sides 30 1 30
Triangles 4 all sides must not be equal 20 1 20

One construction is shown at the top of the page. Due to the computer solution I placed the pieces like a net for the solid. After this two parts of the "sphere" were constructed so that they could be combined to get the whole solid.

The obj-files for the 62 polygons are here.

Truncated Cuboctahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
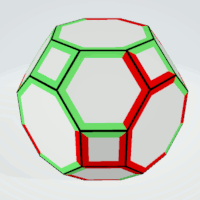Octagons 2 exactly two equal sides
not opposite		 6 1 6
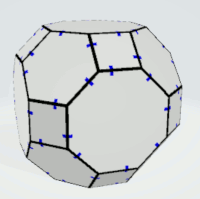Hexagons 2 four or five equal sides 8 1 8
Squares 2 - 6 2 12
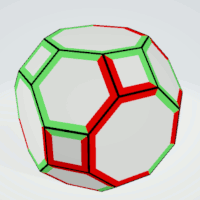Octagons 2 exactly two equal sides
not neighboring		 6 1 6
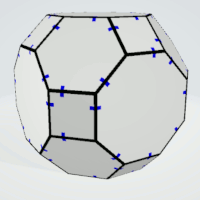Hexagons 2 four or five equal sides 8 1 8
Squares 2 - 6 2 12

Truncated Tetrahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
Hexagons 2 two pairs of three equal sides 4 1 4
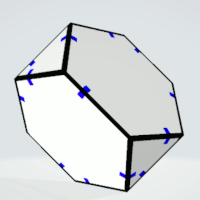Triangles 2 exactly two equal sides 2 2 4
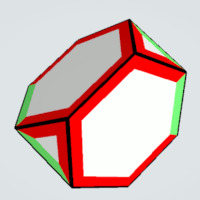Hexagons 2 exactly five equal sides 2 2 4
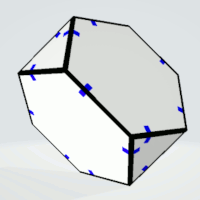Triangles 2 exactly two equal sides 2 2 4
no solution Hexagons 2 at least five equal sides 4 1 4
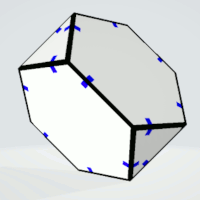Triangles 2 exactly two equal sides 2 2 4

Truncated Octahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
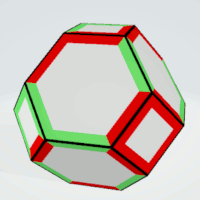Hexagons 2 two pairs of three equal sides 4 2 8
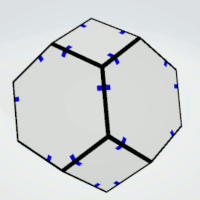Squares 2 - 6 1 6
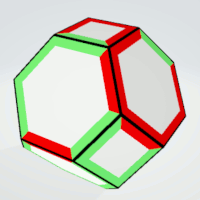Hexagons 2 four or five equal sides 8 1 8
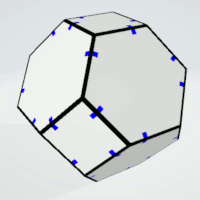Squares 2 - 6 1 6

Truncated Dodecahedron

Polygons Used Colors or
Positions of Marks		 Restrictions on the Polygons Possible Pieces Sets All Pieces
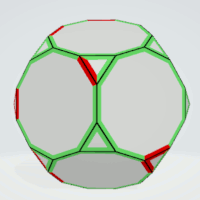Decagons 2 eight or nine equal sides 12 1 12
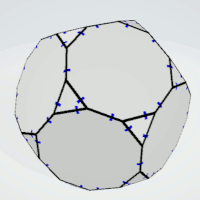Triangles 2 - 4 5 20
Home